Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 38
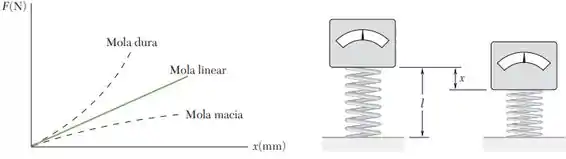
Molas não lineares são classificadas como duras ou macias, dependendo da curvatura de sua curva força-deflexão (ver a figura). Se um instrumento delicado, com massa de 5 kg, é colocado sobre uma mola de comprimento , de modo a que sua base esteja apenas tocando a mola indeformada, sendo então liberado do repouso inadvertidamente, determine a máxima deflexão da mola e a máxima força exercida pela mola, considerando (a) mola linear de constante , (b) mola dura, não linear, para a qual .
Passo 1
Vamos lá! Como estamos em um capítulo que trabalha com trabalho e energia, vamos utilizar esta metodologia para resolver esta questão!
Esta questão possui um ponto bastante interessante. A metodologia utilizada para resolver a letra a) é exatamente a mesma que a da letra b). A única diferença está na equação da força elástica .
Em ambos os casos queremos determinar a deflexão máxima e a força máxima . Mas, para isto, nosso primeiro passo é construir um diagrama de corpo livre. Então, fazendo o diagrama de corpo livre, temos,
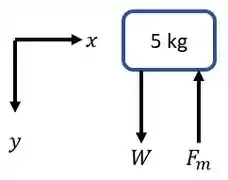
Passo 2
Vamos começar resolvendo a letra a) inicialmente. Aqui, a força da mola é .
Agora, vamos determinar os componentes de energia e trabalho para utilizarmos o princípio do trabalho e energia.
No ponto inicial, em que a mola não está deformada, o bloco tem velocidade zero (parte do repouso). Já no ponto final, ele terá velocidade . Portanto, as energias cinéticas são:
Agora, temos que calcular o trabalho das forças sobre o bloco. Ele será:
Passo 3
Agora já temos todas as informações necessárias para calcularmos a deflexão máxima e força máxima para a mola linear. A deflexão será quando a velocidade do ponto 2 for igual a zero. Assim, aplicando o princípio do trabalho e energia, temos:
Resolvendo a equação acima obtemos . E para a força da mola máxima, como a mola é linear, ela será no ponto de máxima deformação. Portanto,
E assim finalizamos a letra a).
Passo 4
Para a letra b), temos que realizar o mesmo procedimento, só que para a força dada no enunciado da questão. Portanto, calculando o trabalho das forças, temos:
Continuando, a deflexão será quando a velocidade do ponto 2 for igual a zero. Assim, aplicando o princípio do trabalho e energia, temos:
Resolvendo a equação acima, obtemos que .
Passo 5
Já para o cálculo da força máxima, precisamos utilizar as ferramentas de cálculo. Assim, vamos derivar a função da força e igualar a zero para analisar o ponto crítico.
Caso este esteja entre 0 e 0,0304 m, então, a força será máxima neste ponto. Caso contrário, a força será máxima no ponto .
Desta forma, derivando a função força, temos:
Resolvendo a equação acima obtemos . Como este valor é maior que , então, a força máxima será neste valor (limite do intervalo). Assim, obtemos:
E assim finalizamos a nossa questão.