Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 33

Uma mesa de servir uniforme com 5 kg é apoiada em cada lado por pares de ligações idênticas , AB e CD, e molas CE. Se a tigela tem uma massa de 1 kg, determine o ângulo θ onde a mesa está em equilíbrio. As molas têm uma rigidez k = 200   N / m cada uma e estão livres quando θ = 90 º . Despreze a massa das ligações.

Passo 1

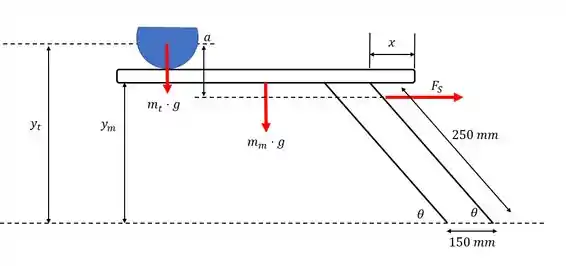
Desenhando o diagrama do corpo livre:

Passo 2

Da geometria da figura, vemos que:

y = 250 s e n θ 1000 = 0,25 s e n θ x = C D ⋅ c o s θ ⇒ x = 0,25 c o s θ

Passo 3

Agora vamos escrever a expressão da energia potencial total do sistema:

V = V m e s a + V t i g e l a + V m o l a V = V m + V t + V s  

Passo 4

Calculando as energias potenciais individuais:

Mesa:

V m = m m ⋅ g ⋅ y V m = 5 ⋅ 9,81 ⋅ y V m = 49,05 y = 49,05 ⋅ 0,25 s e n θ V m = 12,26 s e n θ

Tigela:

V t = m t ⋅ 9,81 ⋅ y V t = 1 ⋅ 9,81 ⋅ y V t = 9,81 y = 9,81 ⋅ 0,25 c o s θ = 2,45 s e n θ

Mola:

As molas estão livres para θ = 90 º . Numa posição qualquer, as molas são esticada de x , sendo x = 0,25 c o s θ

V s = 2 × 1 2 k x 2 V s = 2 × 1 2 ⋅ 200 ⋅ 0,25 c o s θ - 0 2 = 12,5 cos 2 ⁡ θ

Passo 5

Para achar a posição de equilíbrio, tomamos a primeira derivada da energia potencial total do sistemma e igualamos a 0:

V = V m + V t + V s = 12,26 c o s θ + 2,45 c o s θ + 12,5 cos 2 ⁡ θ V =   14,71 s e n θ + 12,5 cos 2 ⁡ θ

d V d θ = 14,71 c o s θ + 2 ⋅ 12,5 ⋅ c o s θ ( - s e n θ )

d V d θ = 14,71 c o s θ - 25 s e n θ c o s θ = c o s θ 14,7 - 25 s e n θ

A posição de equilíbrio ocorre para:

- s e n θ 14,71 + 25 c o s θ = 0 c o s θ = 0 ⇒ θ = 90 º 14,71 + 25 s e n θ = 0   ⇒ s e n θ =   14,71 25 = 0,588 ⇒ θ = a r c s e n 0,588 = 36,1 º  

Passo 6

Analisando a estabilidade:

Para θ = 90 º : d 2 V d θ 2 = - 14,71 s e n θ - 25 cos 2 ⁡ θ + 25 s e n 2 θ = - 14,71 - 0 + 25 = 10,29 > 0   ⇒ e s t á v e l

Para θ = 36,1 º   : d 2 V d θ 2 = - 14,71 s e n θ - 25 cos 2 ⁡ θ + 25 s e n 2 θ = - 16,31 < 0   ⇒ i n s t á v e l

Resposta

θ = 90 º   ( e s t á v e l )

θ = 36,1 º   ( i n s t á v e l )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra uniforme OA tem um peso de 100 N e quando ela está na posição vertical, a mola está livre. Determine a posição θ para o equilíbrio. Investigue a estabilidade na posição de equilíbrio.
A barra uniforme tem um peso W . Determine o ângulo θ para o equilíbrio. A mola está livre quando θ = 90 ° . Despreze o peso dos roletes.
Resolva o problema 11.56 usando o princípio de energia potencial. Investigue a estabilidade da barra quando ela está na posição de equilíbrio.
Determine a altura h do bloco B de modo que a barra esteja sempre em equilíbrio. As molas estão livres quando a barra está na posição vertical. O bloco tem um peso W .
Um furo cônico é perfurado no fundo do cilindro, e depois é apoiado na barra em A . Determine a distância mínima d a fim de que ele permaneça em equilíbrio estável.