Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 43
A barra uniforme de é montada em um mancal em e está suspensa em uma posição vertical. O mancal está montado em suportes elásticos rígidos, instrumentados com extensômetros elétricos calibrados para registrar a força horizontal aplicada ao mancal em . Se os extensômetros registram um valor máximo de durante a aplicação súbita da força horizontal aplicada na extremidade da barra, calcule o valor máximo de .
Passo 1
Vamos supôr que a barra adquire uma aceleração angular . Nesse caso podemos escrever o seguinte:
E por conveniência, vamos considerar essa equação em relação ao centro de massa da barra.
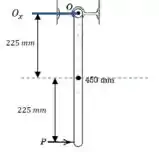
E vamos tomar o sentido anti-horário como positivo:
E o momento de inércia em relação ao centro de massa da barra é:
Então:
Passo 2
Temos duas incógnitas, e , mas apenas uma equação. Precisamos encontrar outra. Já fizemos uma equação de momentos, vamos escrever uma de forças:
Se a barra se move com aceleração angular em torno do ponto , então a aceleração tangencial (no instante em que a força começa a agir) do centro de massa é:
E as forças que atuam nessa direção são as mesmas de antes:
E essa é nossa segunda equação. Com ela completamos um sistema que pode ser resolvido para encontrar :
Agora vamos isolar na segunda equação e substituir na primeira:
E como calculamos isso supondo o valor máximo de , esse também é o valor máximo da força .
Resposta
O valor máximo de é .