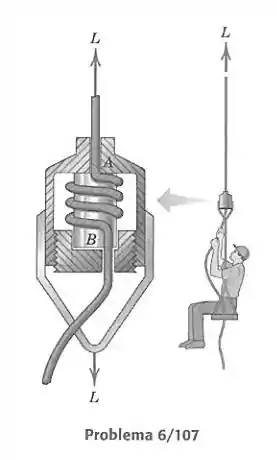
Um dispositivo projetado para abaixar por meio de uma corda, a uma taxa constante controlada, uma pessoa sentada em um banco está mostrado na figura. A corda passa em torno de um eixo central preso à armação e sai livremente pelo anel inferior. O número de voltas é ajustado girando-se o anel inferior, que enrola ou desenrola a corda em torno do eixo. A entrada da corda na parte superior do dispositivo, em , é equivalente a ¼ de uma volta, e a passagem em torno da extremidade, em , também é equivalente a ¼ de uma volta. O atrito da corda nos canais de entrada e saída é, em média, de 10 N por canal. Se três voltas completas em torno do eixo, além das voltas nas extremidades, são necessárias para que um homem de 75 kg se abaixe a uma taxa constante sem puxar a extremidade livre da corda, calcule o coeficiente de atrito entre a cirda e as superfícies de contato do dispositivo. Despreze o pequeno ângulo de hélice da corda em torno do eixo.

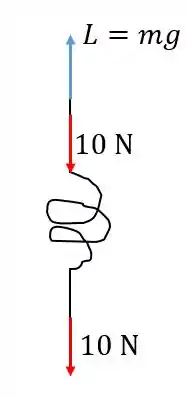
Primeiro vamos definir os valores das trações e . A tração menor é de 10 N, que é a força que puxa a corda para baixo no canal de baixo, tentando impedi-la de subir. A tração é feita pelo peso do homem, menos 10 N, pois o canal faz essa força tentando puxar a corda de volta para o eixo.

Agora aplicaremos a fórmula. O ângulo total é de três voltas mais dois quartos de volta:

Então: