Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 44
O anel esguio de 15 kg atinge o degrau de 20 mm de altura. Determine a menor velocidade angular que o anel pode ter, de maneira que ele vá simplesmente rolar sobre o degrau em A sem deslizar.
Passo 1
Começaremos o exercício aplicando a conservação da quantidade de movimento angular entre os instantes 1 e 2 com o auxílio da imagem a seguir:
Passo 2
Agora iremos analisar o instante em que o anel esguio toca o ponto A, aplicando um equilíbro de forças na direção normal com o auxílio da imagem a seguir:
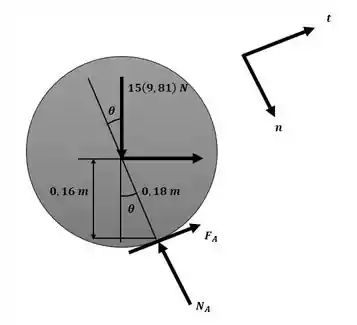
Passo 3
No instante em que o anel está para rebater no ponto A, , e conforme a imagem do passo 2:
Substituindo esse valor na última equação do passo 2:
E agora substituindo esse valor na relação encontrada no passo 1:
Resposta
Exercícios de Livros Relacionados
Um bloco B de 1,5k g está preso a uma mola indeformada de constante k = 80N / m e repousa sobre uma superfície horizontal sem atrito, quando é atingido por um bloco A idêntico movendo-se a uma velocid
O bloco A é liberado do repouso e desliza para baixo na superfície de B sem atrito até atingir um batente na extremidade direita de B . O bloco A tem uma massa de 10k g e o objeto B de massa de 30k g
Uma esfera A de 1k g é solta de uma altura de 5,909m sobre uma placa B de 2k g , que é suportada por um conjunto acondicionado de molas e que inicialmente está em repouso. Sabendo que o coeficiente de
Uma esfera dá o rebote mostrado na figura após atingir um plano inclinado com uma velocidade vertical v 0 de intensidade 15m / s . Sabendo que α = 30 ° e e = 0,8 entre a esfera e o plano, determine a
Um bloco B de 1k g move-se com velocidade v 0 de intensidade 2m / s quando bate na esfera A de 0,5k g , que está em repouso e pendurada por uma corda presa em O. Sabendo que u = 0,6 entre o bloco e a