Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 145

Mostre que um torsor pode ser susbtituido por duas forças perpendiculares, uma das quais é aplicada em um dado ponto.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos o seguinte arranjo:

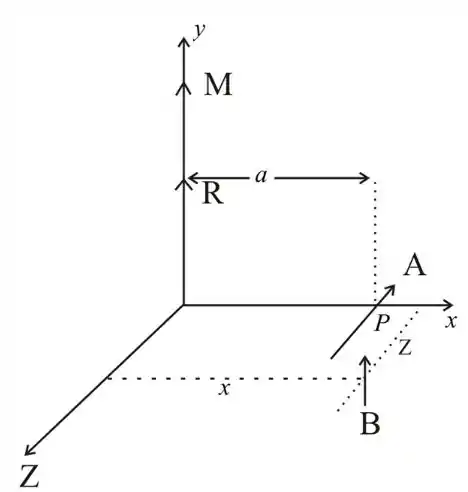
Vamos expressar a resultante R e o momento M como:

R = R j

M = M j

Passo 2

Agora, vamos expressar as forças A e B :

A = A x i + A y j + A z k

Vamos considerar B no plano x z :

B = B x i + B y j + B z k

Vamos calcular as forças pra o sistema equivalente:

∑ F x = 0

A x + B x = 0

B x = - A x

∑ F y = 0

A y + B y = R

E:

∑ F z = 0

A z + B z = 0

B z = - A z

Passo 3

Vamos calcular o momento na direção x :

∑ M x = 0

z B y = 0

Agora em y :

∑ M y = 0

- a A z - x B z + z B x = M

Agora em z :

∑ M z = 0

a A y + x B y = 0

Portanto:

x = - a A y B y

Passo 4

Como A e B são perpendiculares, temos que:

A ⋅ B = 0

Portanto:

A x i + A y j + A z k ⋅ B x i + B y j + B z k = 0

Sabemos que em um produto escalar entre vetores, nós temos que multiplicar os vetores do mesmo eixo, logo:

A x ⋅ B x + A y ⋅ B y + A z ⋅ B z = 0

Já descobrimos que B y = 0 ou z = 0 , portanto, vamos testar primeiro para B y = 0 :

A x ⋅ B x + A z ⋅ B z = 0

Passo 5

Temos que:

B x = - A x

E:

B z = - A z

Substituindo na equação do passo anterior temos que:

- A x 2 - A z 2 = 0

Veja que as componentes de A devem ser reais, a solução da equação resultaria em uma componente imaginária, portanto, temos que:

B y ≠ 0

E:

z = 0

Passo 6

Vimos que existem infinitas soluções para o problema. Vamos considerar A x = 0 . Deste modo podemos encontrar uma solução única.

Como A x = 0 , temos que:

B x = - 0

B x = 0

Logo:

- a A z - x B z + z 0 = M

- a A z - x B z = M

Temos que:

0 ⋅ B x + A y ⋅ B y + A z ⋅ B z = 0

A y ⋅ B y + A z ⋅ B z = 0

E sabemos também que:

A y = R - B y

Passo 7

Agora temos todas as equações necessárias. Vamos substituir para encontrar as componentes de A e B .

- a A z - x B z = M

- a A z - - a A y B y - A z = M

- a A z - - a R - B y B y - A z = M

Logo:

A z = - M B y a R

Temos também que:

A y ⋅ B y + A z ⋅ B z = 0

R - B y B y + - M B y a R M B y a R = 0

Logo:

B y = a 2 R 3 a 2 R 2 + M 2

Outra relação é:

A y = R - B y

Logo:

A y = R - a 2 R 3 a 2 R 2 + M 2

A y = M 2 R a 2 R 2 + M 2

E:

A z = - M a R a 2 R 3 a 2 R 2 + M 2

A z = a R 2 M a 2 R 2 + M 2

A ultima incógnita a ser descoberta é B z . Temos que:

B z = M B y a R

B z = a 2 R 2 M a 2 R 2 + M 2

Passo 8

Portanto:

A = A x i + A y j + A z k

A = 0 i + M 2 R a 2 R 2 + M 2 j + a R 2 M a 2 R 2 + M 2 k

A = R M a 2 R 2 + M 2 M j - a R k

E:

B = B x i + B y j + B z k

B = 0 i + a 2 R 3 a 2 R 2 + M 2 j + a R 2 M a 2 R 2 + M 2 k

B = a R 2 a 2 R 2 + M 2 a R j + M k

Resposta

A = R M a 2 R 2 + M 2 M j - a R k

B = a R 2 a 2 R 2 + M 2 a R j + M k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três forças atuam no ponto O . Determine F 3 , θ e R , se é conhecido que a componente y da força resultante R → vale - 5k N e que a componente z vale 6k N .
O avião de passageiros do problema 2 / 68 está redesenhado aqui com informações tridimentionais. Se a turbina 3 falha subitamente, determine a resultante dos vetores de empuxo das três turbinas remane
Determine o sistema força-binário em O , que seja equivalente às duas forças aplicadas ao eixo A O B . R → é perpendicular a M → O ?
A polia e a engrenagem estão submetidas às cargas mostradas. Para estar forças, determine o sistema força-binário equivalente no ponto O .
Duas cargas direcionadas para cima são exercidas sobre uma pequena treliça tridimensional. Reduza estas duas cargas a um único sistema força-binário no ponto O . Mostre que R → é perpencidular a M → O