Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 113

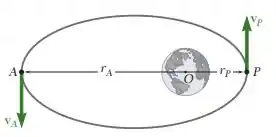
Mostre que os valores v A e v P da velocidade de um satélite da Terra no apogeu A e no perigeu P de uma órbita elíptica estão definidos pelas relações

v A 2 = 2 G M r A + r P r P r A                               v P 2 = 2 G M r A + r P r A r P

onde M é a massa da Terra e r A e r P representam, respectivamente, as distâncias máxima e mínima da órbita ao centro da Terra.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora para mais uma questão de Dinâmica. Nesta questão temos que mostrar que as velocidades v A e v P de um satélite são dados pelas seguintes relações:

v A 2 = 2 G M r A + r P r P r A                               v P 2 = 2 G M r A + r P r A r P

Para isso, vamos primeiro utilizar a relação de conservação de momento angular, dada por:

r A m v A = r P m v P v A = r P r A v P             ( 1 )

Em seguida, vamos utilizar a conservação de energia, neste caso, temos:

1 2 m v P 2 - G M m r P = 1 2 m v A 2 - G M m r A             ( 2 )

Com isso, a gente ficou com um sistema linear de duas equações e duas incógnitas. Bora substituir a equação ( 1 ) na equação ( 2 ) . Fica assim:

1 2 m v P 2 - G M m r P = 1 2 m v A 2 - G M m r A 1 2 m v P 2 - G M m r P = 1 2 m r P r A v P 2 - G M m r A

Fazendo algumas manipulações algébricas, temos:

1 - r P r A 2 v P 2 = 2 G M 1 r P - 1 r A r A 2 - r P 2 r A 2 v P 2 = 2 G M   r A - r P r A r P r A 2 - r P 2 = r A - r P r A + r P   v P 2 = 2 G M r A + r P r A r P

Opa, provamos que a relação para a velocidade no perigeu v P   que o enunciado nos deu é verdadeira. Para encontramos a velocidade no apogeu, vamos substituir essa relação na equação ( 1 ) que encontramos:

v A = r P r A v P

Substituindo:

v A = r P r A v P 2 = 2 G M r A + r P r A r P v A 2 = 2 G M r A + r P r P r A

É isso, galera. Conseguimos provar que a velocidade no apogeu também é verdadeira. Bora zerar esse livro!

Resposta

v P 2 = 2 G M r A + r P r A r P

v A 2 = 2 G M r A + r P r P r A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma mola é usada para parar um pacote de 50 kg que está se movendo para baixo numa inclinação de 20°. A mola tem constante k = 30 kN/m e é mantida por cabos de modo que está comprimida inicialmente de
É mostrado na mecânica dos materiais que quando uma viga elástica AB suporta um bloco de peso W em um ponto B, a deflexão y e s t (chamada de deflexão estática) é proporcional a W. Mostre que se o mes
Um colar de 1,3 kg pode deslizar ao longo da barra mostrada na figura. Ele está preso a uma corda elástica fixada em F que tem um comprimento indeformado de 0,9 m e uma constante de mola de 60 N/m. Sa
Um colar de 3 kg pode deslizar sem atrito sobre uma barra vertical e ficar em repouso equilibrando-se sobre uma mola. Ele é empurrado para baixo, comprimindo a mola 150 mm e é liberado. Sabendo que a
Um colar de 500 g pode deslizar sem atrito sobre uma barra curva BC em um plano horizontal. Sabendo que o comprimento indeformado da mola é de 80 mm e que k = 400 kN/m, determine (a) a velocidade que