Um vagão de carvão com uma massa de vazio está se deslocando livremente com uma velocidade de sob um funil de enchimento que se abre e libera o carvão no vagão em movimento à taxa constante de por segundo. Determine a distância percorrida pelo vagão durante o intervalo de tempo em que de carvão são depositadas no vagão. Despreze qualquer resistência por atrito no rolamento ao longo do trilho horizontal.
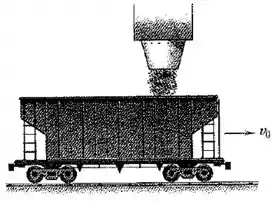
Passo 1
Como o vagão está se movendo livremente, podemos ter certeza de que a soma das forças externas é nula. Então:
Onde é o momento linear do vagão:
Perceba que a velocidade de queda do carvão nem aparece na nossa conta, porque está na direção vertical, e estamos analisando apenas a horizontal.
Passo 2
Vamos encontrar uma expressão para a massa do vagão em função do tempo:
Vamos voltar para nossa equação lá de cima:
E é a aceleração do carrinho:
Mas nosso objetivo é encontrar uma função para o deslocamento em função do tempo. Vamos começar reescrevendo a aceleração:
E então nossa equação se torna uma EDO separável:
Passo 3
Em seguida vamos resolver essa equação diferencial. Precisamos integrar com indo da velocidade inicial até um valor de , e com o tempo indo de até um instante .
E aplicando a expontencial nos dois lados:
Passo 4
Beleza, agora precisamos transformar isso em uma função para a posição em relação ao tempo. Precisamos reescrever a velocidade:
E agora integramos mais uma vez, com variando de até uma posição qualquer, e variando novamente de até um instante qualquer :
E podemos reorganizar um pouco:
Passo 5
Nosso objetivo final é calcular o deslocamento no instante em que a massa de carvão depositada atinge . Como a máquina despeja toneladas a cada segundo:
Agora é só substituir na equação com os valores numéricos que foram dados no enunciado:
Resposta
O vagão percorre durante esse intervalo de tempo.