Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 5
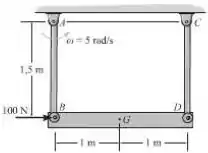
No instante mostrado, ambas as barras de massa desprezível balançam com uma velocidade angular no sentido anti-horário , enquanto a barra de está sujeita à força horizontal de . Determine a tração desenvolvida nas barras e a aceleração angular das barras nesse instante.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O exercício nos pede a tração desenvolvida nas barras e a aceleração angular das barras.
Vamos à análise tangencial:
Temos que:
Logo:
Passo 2
Para a análise dinâmica das forças normais, temos:
Temos que:
Logo:
A análise do momento para o centro de massa nos dará outra equação:
Ou seja:
Resposta
Exercícios de Livros Relacionados
Utilize os resultados do Prob. 7/55 e determine a quantidade de movimento angular H g dobrada daquele problema em relação ao seu centro de massa G utilizando os eixos de referência fornecidos.
O disco circular uniforme do Prob. 7/48, com três componentes de velocidade angular, é mostrado novamente aqui. Determine a energia cinética T e a quantiadde de movimento angular H o , para o instante
O eixo esbelto sustenta duas partículas descoladas, cada uma de massa m, e gira em relação ao eixo z com velocidade angular constante ω conforme indicado. Determine as componentes x e y das reações no
A barra esbelta uniforme de comprimento l e massa m está soldada ao eixo, que gira apoiado nos mancais A eB com um velocidade angular constante ω . Determine a espressão para a força suportada pelo ma
O mecanismo para controlar a implantação de um painel solar de uma nave espacial a partir da posição A para a posição B está sendo projetado. Determine a expressão vetorial para o único ângulo θ de ro