Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 42

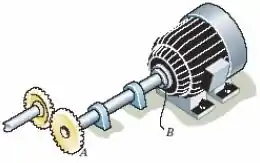
O motor transmite 400 kW ao eixo de aço AB, o qual é tubular e tem diâmetro externo de 50 mm e diâmetro interno de 46 mm. Determine a menor velocidade angular com a qual ele pode girar se a tensão de cisalhamento admissível para o material for T a d m =   175   M P a .

Passo 1

Antes de colocarmos a mão na massa, vamos listar os dados que nós temos:

P = 400 k W = 400 × 10 3 w

d 0 = 50 m m = 0,050 m

d i = 46 m m = 0,046 m

T a d m = 175 M P a = 175 × 10 6 N m 2

Neste problema, sabendo os valores da potência e dos diâmetros externo e interno, precisamos determinar a menor velocidade angular ( ω ) com a qual o eixo de aço AB pode girar se a tensão de cisalhamento admissível para o material for T a d m =   175   M P a , certo?

Confiem em mim essa questão é bem tranquila. Vou dar um spoiler do que iremos fazer para matá-la.

Inicialmente, vamos encontrar o valor de T , para isso utilizaremos a fórmula da τ m á x :

τ m á x = T m á x × c J

Com o valor de T em mãos e sabendo que P = T × ω , fica fácil determinarmos quem é ω .

Então, vamos lá?

Passo 2

Utilizando a fórmula da τ m á x para encontrar T , temos:

τ m á x = T m á x × c J

Isolando T m á x :

T m á x = τ m á x × J c

Sendo J o nosso momento polar de inércia, que é dado por:

J = π 2 × c 4

Notem que como o eixo de aço AB é tubular, para calcular o valor de J devemos subtrair do diâmetro externo elevado à quarta o valor do diâmetro interno elevado à quarta.

J = π 2 × c e x t 4 - π 2 × c i n t 4

J = π 2 × ( c e x t 4 - c i n t 4 )

J = π 2 × 0,025 m 4 - 0,023 m 4

J = 1,74 × 10 - 7   m 4

Vamos atribuir valores à fórmula:

T m á x = τ m á x × J c

Lembrando que c é a maior distância no tubo ou seja

c = 0,05 2 = 0,025   m

T m á x = 175 × 10 6 × 1,74 × 10 - 7 0,025 m

T m á x = 1218,134 N . m  

Passo 3

A fórmula da potência depende do torque e nos permite calcular a velocidade angular do sistema:

P = T × ω

Ou seja, potência é igual ao torque vezes a velocidade angular. Podemos reorganizar da forma:

ω = P T

Os valores de P e T são conhecidos, substituindo os na fórmula, temos:

ω = P T

ω = 400 × 10 3 1218,134

ω = 328,37   r a d / s  

Para achar o valor em RPM temos de multiplicar por 60 porque estamos passando de segundos para minutos e dividir por 2 π porque estamos passando de r a d para r e v o l u ç õ e s :

ω = 328,37 × 2 π   r a d 60   s  

ω = 3135,70 r e v o l u ç õ e s m i n u t o = 3135,70   r p m

Executamu mais uma. VAPO!

Resposta

ω = 3135,70 R P M

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O motor de engrenagens pode desenvolver 100W quando gira a 300rev/minuto . Se o eixo tiver diâmetro de 12mm , determine a tensão de cisalhamento máxima que será desenvolvida no eixo.
O motor transmite um torque de 50Nm ao eixo A B . Esse torque é transmitido ao eixo C D pelas engrenagens em E e F . Determine o torque de equilíbrio T ' no eixo C D e a tensão de cisalhamento máxima
O motor de engrenagens pode desenvolver 100W quando gira a 80rev/minuto . Se a tensão de cisalhamento admissível para o eixo for τ A d m = 28MPa , determine, com aproximação de múltiplos de 5mm , o me
Se o torque aplicado ao eixo C D for T ' = 75Nm , determine a tensão de cisalhamento máxima absoluta em cada eixo. Os mancais B , C e D permitem livre rotação dos eixos, e o motor impede a rotação dos
O moto-redutor de 2,5kW pode girar a 330rev/minuto . Se o diâmetro do eixo for 20mm , determine a tensão de cisalhamento máxima que será desenvolvida no eixo.