Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 131

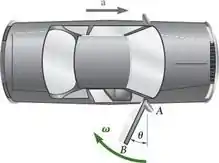
Um motorista liga seu carro com a porta do lado do passageiro totalmente aberta ( θ = 0). A porta de 40 kg tem raio de giração em torno do centro de massa k = 300 mm e seu centro de massa está localizado a uma distância r = 500 mm de seu eixo vertical de rotação. Sabendo que o motorista mantém uma aceleração constante de 2 m/s2, determine a velocidade angular da porta quando ela bate ao fechar ( θ = 90°).

Passo 1

Cinemática:

a = a A

Onde

a G / A t = r _ α     θ

Cinética:

+ Σ M A = Σ M A e f f :             0 = I _ α + m r _ α r _ - m a A r _ c o s c o s   θ  

m k _ 2 α + m r _ 2 α = m a A r _ c o s c o s   θ  

α = a A r _ k _ 2 + r _ 2 c o s c o s   θ  

Passo 2

Definindo α = ω d ω d θ , e usando r _ = 22 12   f t ,   k _ = 125 12   f t

ω = d ω d θ = 22 12 f t a A 12.5 12 f t 2 + 22 12 f t 2 c o s c o s   θ  

= 0.41234 a A c o s c o s   θ  

ω d ω = 0.41234 a A c o s c o s   θ   d θ  

∫ 0 ω f ω d ω = ∫ 0 π / 2 0.4124 a A c o s c o s   θ   d θ  

1 2 ω 2 0 ω f = 0.41234 a A s i n s i n   θ   0 π / 2

ω f 2 = 0.82468 a A

Passo 3

Dados fornecidos:

a A = 2   m / s 2 →

ω f 2 = 0.82468 2 = 1,649   r a d / s

Resposta

ω f = 1,649   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

54. O pinhão A roda sobre a cremalheira fixa B com uma velocidade angular ω = 4 r a d s . Determine a velocidade da cremalheira C.
O anel semicircular uniforme de massa m = 2,5k g e raio médio r = 200m m está montado sobre raios de massa desprezível e gira em torno de um eixo horizontal através de O . Se o anel é liberado a parti
O cilindro maciço homogêneo possui uma massa de 100k g e está montado em um eixo em ângulo reto que gira livremente em torno do eixo horizontal O - O . Se o cilindro é liberado a partit do repouso com
A massa da engrenagem A é de 20k g e seu raio de giração centroidal é de 150m m . A massa da engrenagem B é de 10k g e seu raio de giração centroidal é de 100m m . Calcule a aceleração angular da engr
O anel semicircular de massa m e raio r está soldado no eixo vertical, que permite que o anel gire no plano horizontal em torno do eixo O - O . Se um torque M é aplicado ao anel por meio de seu eixo,