Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 175

O movimento do pino P é restringido pela fenda curva da lemniscata em O B e pela fenda do braço O A . Se O A gira no sentido anti-horário com uma velocidade angular de θ ˙ = 3   r a d / s , determine a intensidade da velocidade e aceleração do pino P em θ = 30 ° .

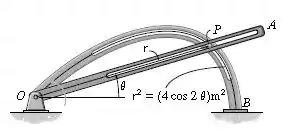
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O enunciado nos pede as intensidades da velocidade e aceleração do pino P no instante em que θ = 30 ° .

As intensidades são dadas por:

v = v r 2 + v θ 2

a = a r 2 + a θ 2

Nos é dada a equação da posição:

r 2 = 4 cos ⁡ 2 θ

Vamos derivar essa equação dos dois lados:

d d t ( r 2 ) = d d t ( 4 cos ⁡ 2 θ )

2 r d r d t = - 4 2 sin ⁡ 2 θ d θ d t

2 r r ˙ = - 8 sin ⁡ 2 θ θ ˙

Logo:

r ˙ = - 4 sin ⁡ 2 θ θ ˙ r

Agora temos que encontrar a equação para a aceleração:

d d t ( 2 r r ˙ ) = d d t ( - 8 sin ⁡ 2 θ θ ˙ )

Note que agora temos que aplicar a regra do produto na derivação pois temos r multiplicando r ˙ , e cos ⁡ 2 θ multiplicando θ ˙ .

A regra do produto é aplicada quando é necessário fazer a derivada do produto de equações.

Logo:

2 1 d r d t r ˙ + r d r ˙ d t = - 8 2 cos ⁡ 2 θ d θ d t θ ˙ + sin ⁡ 2 θ d θ ˙ d t

2 r ˙ r ˙ + r r ¨ = - 8 2 cos ⁡ 2 θ θ ˙ θ ˙ + sin ⁡ 2 θ θ ¨

r ˙ 2 + r r ¨ = - 8 cos ⁡ 2 θ θ ˙ 2 - 4 sin ⁡ 2 θ θ ¨

Queremos a aceleração dada por r ¨ , logo:

r ¨ = - 4 sin ⁡ 2 θ θ ¨ - 8 cos ⁡ 2 θ θ ˙ 2 - r ˙ 2 r

Passo 2

Agora que já descobrimos as equações que vamos precisar, é só aplicar os dados do enunciado, ou seja, quando θ = 30 ° , θ ˙ = 3   r a d / s e θ ¨ = 0   r a d / s 2 :

r θ = 30 ° = 4 cos ⁡ 60 °

r θ = 30 ° = 2   m

r ˙ θ = 30 ° = - 4 sin ⁡ ( 6 0 ° ) ( 3 ) 2

r ˙ θ = 30 ° = - 7,348   m / s

r ¨ θ = 30 ° = - 4 sin ⁡ 60 ° 0 - 8 cos ⁡ 60 ° 3 2 - - 7,348 2 2

r ¨ θ = 30 ° = - 63,64   m / s 2

Agora temos todos os dados necessários para resolver nosso problema.

Os valores de v r e v θ são dados por:

v r = r ˙

v θ = r θ ˙

Logo:

v r = - 7,348   m / s

E:

v θ = 2 3

v θ = 4,243   m / s

Os valores de a r e a θ são dados por:

a r = r ¨ - r θ ˙ 2

a θ = r θ ¨ + 2 r ˙ θ ˙

Logo:

a r = - 63,64 - 2 3 2

a r = - 76,37   m / s 2

E:

a θ = 2 0 + 2 ( - 7,348 ) ( 3 )

a θ = - 44,09   m / s 2

Passo 3

As magnitudes solicitadas nas questões valem:

v = v r 2 + v θ 2

v = - 7,348   2 + 4,243 2

v = 8,49   m / s

E:

a = a r 2 + a θ 2

a = - 76,37 2 + - 44,09 2

a = 88,2   m / s 2

DICA IMPORTANTE!!!

Questões desse tipo, que envolvem derivada de vários termos e regra do produto, é importante ter bastante atenção, pois quando erramos um termo, a questão vai toda por água abaixo. Portanto tenha calma e resolva passo a passo.

Resposta

v = 8,49   m / s

a = 88,2   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A pequena arruela desliza para baixo na corda OA. Quando ela está no meio do caminho, sua velocidade escalar é 200 mm/s e sua aceleração é 10mm/s². Expresse a velocidade e a aceleração da arruela ness
Um carro move-se ao longo da curva circular tendo um raio r = 120 m. No instante mostrado, sua taxa angular de rotação é θ ˙ = 0,025r a d / s , que está diminuindo na razão de θ ¨ = - 0,08r a d / s 2
Um carro de corrida move-se ao longo da pista circular com uma velocidade escalar de 16 m/s. Quando ele chega ao ponto A , ele aumenta sua velocidade escalar na razão de a t = ( 4 3 v 1 / 4 )m / s 2 ,
Uma motocicleta move-se ao longo da pista elíptica a uma velocidade escalar constante v . Determine a maior intensidade da aceleração se ab .
Uma partícula move-se ao longo da trajetória y = a + b x + c x 2 , onde a , b e c são constantes. Se a velocidade escalar da partícula é constante v = v 0 , determine as componentes x e y da velocidad