Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 155

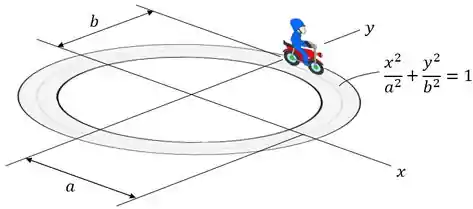
Uma motocicleta move-se ao longo da pista elíptica a uma velocidade escalar constante v . Determine a maior intensidade da aceleração se a > b .

Passo 1

Devemos determinar a maior intensidade da aceleração se a > b .

Sabemos que a velocidade escalar é constante e que a trajetória é dada por

x 2 a 2 + y 2 b 2 = 1

Também sabemos que a aceleração é composta por uma componente tangencial e normal. Estas são:

a t = d v d t

a n = v 2 ρ

E estão relacionadas da seguinte maneira:

a = a t 2 + a n 2

Como a velocidade escalar é constante, a t = 0 e a única varável que afetará no valor da aceleração será o raio de curvatura ρ .

Passo 2

Vamos descobrir o raio de curvatura mínimo para que a aceleração normal seja máxima.

Sabemos que

ρ = 1 + d y d x 2 3 2 d 2 y d x 2

E que x 2 a 2 + y 2 b 2 = 1

Logo, colocando y em evidência, obtemos

y 2 = 1 - x 2 a 2 b 2

y = b a a 2 - x 2  

Onde

d y d x = - b x a a 2 - x 2

d 2 y d x 2 = - a b a 2 - x 2 3 / 2

Substituindo esses valores na fórmula do raio de curvatura, obtemos

ρ = 1 + - b x a a 2 - x 2 2 3 2 - a b a 2 - x 2 3 / 2 = 1 + b 2 x 2 a 2 ( a 2 - x 2 ) 3 2 a b a 2 - x 2 3 / 2

Este valor será mínimo quando o denominador for muito maior que o numerador, ou seja,

1 + b 2 x 2 a 2 ( a 2 - x 2 ) 3 2 ≪ ≪ a b a 2 - x 2 3 / 2

Esta diferença ocorre quando y = 0 e x = a . Portanto, quando x → a ,

1 ≪ ≪ b 2 x 2 a 2 ( a 2 - x 2 )

Portanto, temos que

ρ = b 2 x 2 a 2 ( a 2 - x 2 ) 3 2 a b a 2 - x 2 3 / 2 = b 2 x 2 a 2 ( a 2 - x 2 ) 3 2 a 2 - x 2 3 / 2 a b = b 2 a 4 x 3

Para x = a , temos

ρ = b 2 a 4 ( a ) 3 = b 2 a

Passo 3

A aceleração normal pode então ser determinada.

Sabemos que

a n = v 2 ρ

Logo,

a n m á x = v 2 b 2 a

a n m á x = a v 2 b 2

A intensidade da aceleração máxima será

a m á x = a t 2 + a n 2 m á x

a m á x = 0 + a v 2 b 2 2 = a v 2 b 2

Resposta

a m á x = a v 2 b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Partindo do repouso, o garoto core para fora na direção radial a partir do centro da plataforma com uma aceleração constante de 0,5 m/s². Se a plataforma está girando com uma velocidade constante θ ˙
A fenda do braço OA gira no sentido anti-horário em torno de O com uma velociade angular constante de θ ˙ . O movimento do pino B é restrito de tal maneira que ele se move sobre a superfície circular
Um carro move-se ao longo da curva circular de raio r = 120 m com uma velocidade escalar constante de v = 9 m/s. Determine a taxa angular de rotação θ ˙ da linha radial r e a intensidade da aceleração
Se o braço OA gira no sentido anti-horário com uma velocidade angular constante de θ ˙ = 2r a d / s , determine as intensidades da velocidade e aceleração do pino P em θ = 30 ° . O pino move-se na fen
A fenda do braço OA gira no sentido anti-horário em torno de O de tal maneira que quando θ = π / 4 , o braço OA está girando com uma velocidade angular de θ ˙ e uma aceleração angular de θ ¨ . Determi