Quando o êmbolo de é liberado a partir do repouso em sua guia vertical com , cada mola de rigidez está sem compressão. As conexões são livres para deslizar através de seus cursores articulados e comprimir suas molas. Calcule a velocidade do êmbolo quando a posição é ultrapassada.
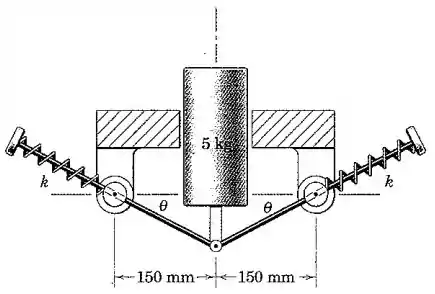
Passo 1
Pela conservação da energia mecânica, temos:
Como a energia cinética inicial é nula, temos:
Passo 2
Já a variação de energia potencial gravitacional deve ser:
Note que deve ser negativo, pois a altura final é menor do que a inicial. Então, olhando para a figura, podemos escrever:
Então:
Passo 3
Por último, a variação da energia potencial elástica é dada por:
pois há duas molas.
Olhando para a figura, podemos calcular a compressão de cada mola:
Então:
Passo 4
Agora que temos cada variação de energia, podemos enfim determinar a velocidade do êmbolo: