Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 114
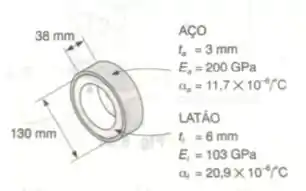
Um anel de latão de de diâmetro externo e espessura de se encaixa perfeitamente dentro de um outro aço de de diâmetro interno e espessura de , quando a temperatura de ambos os anéis é de . Sabendo-se que a temperatura de ambos os anéis é então aumentada para , determinar:
- A tensão normal de tração no anel de aço;
- A correspondente pressão exercida pelo anel de latão sobre o anel de aço.
Passo 1
Fala galerinha, essa questão pode parecer mega complexa, mas vamos ver que ela é bem tranquila e não precisamos ficar preocupados. O que precisamos ver é que usaremos 3 conceitos que já vimos, e que vamos relembrar eles aqui.
Basicamente temos dois anéis cilíndricos, que estão unidos, e com uma variação de temperatura vão ter que variar de tamanho, além dos mais, é exatamente essa variação que vai gerar a tensão, então podemos dizer o seguinte, entre os anéis de aço e latão existe uma pressão de contato, que pode ser definida como:
- O latão empurra o aço para fora, logo o sinal de para o aço é positivo
- O aço, por reação, empurra o latão para dentro, logo a pressão de contato para o latão será dada por .
E como já vimos, a tensão em tubos cilíndricos é dada por:
Em que:
Assim podemos dizer que a tensão de contato em cada anel é dada por:
Passo 2
Agora pensa no seguinte, se temos uma tensão e sabemos que ao anéis vão deformar, vamos precisar dessas deformações, que nesse exemplo se dividem em dois casos, que são as deformações especificas causadas pelas tensões, e as deformações especificas causadas pela temperatura, e assim basta lembrarmos que essas fórmulas são dadas por:
Assim temos que a deformação especifica para cada um dos anéis é dada por:
- Anel de aço
- Anel de Latão
Assim a deformação especifica total do anel de aço é dada por:
Assim a deformação especifica total do anel de aço é dada por:
E pensa no seguinte, isso que calculamos foi a DEFORMAÇÃO ESPECÍFICA, mas sabemos que o que tem que ser igual entre os dois anéis é a VARIAÇÃO DA DEFORMAÇÃO TOTAL, ou seja, basta ,multiplicarmos o comprimento inicial de cada anel pela deformação especifica de cada anel, assim, temos que:
Assim estamos nos encaminhando para o fim do nosso problema, então aguenta mais um pouco para podermos fechar o nosso problema tranquilo.
Passo 3
Agora para fecharmos o nosso problema, sabemos que os anéis estão unidos, por isso eles farão pressão um sobre o outro, e por isso, podemos igualar as variações de deformações entre eles, com isso, teremos que:
Substituindo as nossas deformações especificas, teremos que:
Como nosso objetivo é determinar a carga de contato entre os anéis, teremos que:
Agora só falta os dados para podermos substituir.
Passo 4
Sabemos pelo enunciado que:
Substituindo teremos que:
Então já sabemos a pressão que o anel de latão exerce sobre o anel de aço, e assim resolvemos o item b).
Para o item a) só precisamos lembrar que a nossa fórmula de tensão de tração no aço é dado pela seguinte equação: