Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 44
Um pequeno bloco desliza com uma velocidade sobre uma superfície horizontal a uma altura acima do chão. Determine (a) o ângulo em que ele deixará a superfície cilíndrica , (b) a distância em que ele baterá no chão. Despreze o atrito e a resistência do ar.
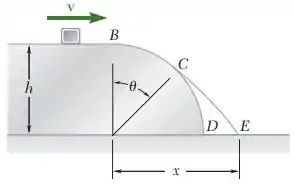
Passo 1
Vamos lá! Esta é uma questão longa, que precisamos dividir em duas partes. Primeiro, precisamos descobrir qual o ângulo em que o bloco irá descolar da superfície. Depois disto, vamos utilizar as equações da cinemática para descobrir o valor de do ponto .
Mas, cada coisa a seu tempo. Vamos começar pelo ângulo . Devemos começar com o seguinte questionamento: o que é necessário acontecer para que o bloco descole da superfície???
Para que isto ocorra, é necessário que a força normal seja nula! Desta forma, vamos começar fazendo o diagrama de corpo livre do nosso problema. Sendo assim, temos:
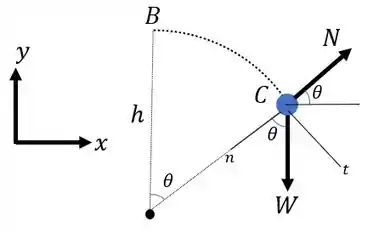
Passo 2
Agora que temos o diagrama de corpo livre, podemos fazer o somatório de forças na direção normal a trajetória. Cuidado para não esquecerem que o bloco possui uma aceleração centrípeta nesta direção!
Sendo assim, temos:
Como assumimos que a força normal é nula neste ponto, temos:
Chegamos assim a nossa primeira relação, entre a velocidade e o ângulo . Precisamos agora de uma segunda equação para resolvermos este enigma!
Passo 3
Nossa segunda equação sairá do princípio de trabalho e energia. Aqui iremos correlacionar o trabalho da força peso (e consequentemente o ângulo ) com a velocidade do bloco.
Desta forma, vamos começar escrevendo as relações de energia cinética e trabalho. Portanto,
Portanto, pelo princípio de trabalho e energia, temos:
E assim conseguimos a nossa segunda equação com as duas incógnitas.
Passo 4
Agora nosso trabalho é resolver o sistema de equação abaixo e descobrir o valor de . Desta forma, temos:
E assim resolvemos a letra a) da nossa questão!
Passo 5
Agora vamos para a letra b) da nossa questão. Devemos aqui determinar o comprimento que o bloco percorre após descolar da superfície.
No ponto , ao descolar, o bloco possui uma velocidade que está na direção tangencial ao movimento. Como determinamos a equação desta velocidade, vamos descobrir agora o seu valor:
Agora, é só decompormos a velocidade na direção e e utilizarmos as equações da cinemática para descobrirmos o tempo . Decompondo a velocidade, temos:
O tempo necessário para que o bloco toque o chão será:
Resolvendo a equação acima descobrimos que o tempo de queda é . Assim, descobrimos que o deslocamento foi:
E assim finalizamos a letra b) e a nossa questão!