Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 52
Um trem de 100.000 kg viaja em uma linha horizontal necessitando de 300 kW para manter constante a velocidade de 80 km/h. Determine (a) a força total necessária para vencer o atrito no eixo das rodas, na resistência ao rolamento e na resistência do ar, (b) a potência adicional necessária se o trem manter a mesma velocidade subindo uma inclinação de 1%
Passo 1
Vamos lá! Temos duas geometrias a analisar aqui. Na letra a), o trem percorre um trecho horizontal. Já na letra b), o mesmo trem, sob as mesmas condições de velocidade e atrito, percorre um trecho inclinado.
Então, vamos começar pelo trecho horizontal identificando quem é a força necessária para vencer o atrito. Para facilitar a visualização, vejamos o seguinte diagrama de corpo livre:
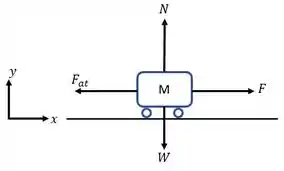
Então, para que o trem esteja em velocidade constante, é necessário que . Portanto, basta calcularmos a força que necessita de uma potência de 300 kW para mantê-la a 80 km/h.
Como a força é constante, temos:
E assim finalizamos a letra a).
Passo 2
Para a letra b) a geometria muda um pouco. Teremos aqui a inclinação 1%, cujo ângulo é:
Então, vamos fazer um outro esboço:
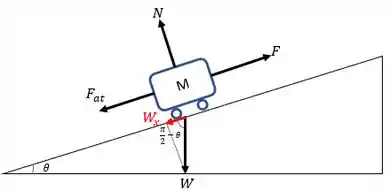
Neste caso o trem continua com velocidade uniforme de 80 km/h. A força de atrito é responsável por consumir uma potência de do trem.
Mas qual é a diferença que um plano inclinado trás? É exatamente a presença da componente do peso. Ela que será a responsável pela potência adicional do trem.
Agora que sabemos a força responsável pela potência adicional, já podemos calculá-la! Logo,
E assim finalizamos a nossa questão!