Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 29

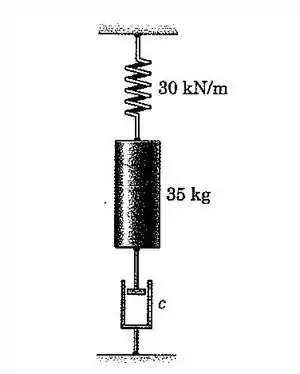
29. Determine o valor do coeficiente de amortecimento viscoso c , para o qual o sistema é criticamente amortecido.

Passo 1

Temos a constante da mola k , igual a 30   k N / m e a massa m do corpo suspenso pela mola. O que isso quer dizer?

Ora bolas, quer dizer que já podemos determinar a frequência angular natural ω n do nosso sistema, a qual é dada pela relação abaixo:

ω n = k m

Substituindo os valores numéricos adequados, chegamos ao seguinte valor:

ω n = 30000   N / m 35   k g

ω n ≅ 29,277   r a d / s

Passo 2

Obtida a frequência natural do sistema, basta agora utilizar a condição para que ocorra amortecimento crítico. Não lembra! Vou refrescar sua memória!

Ocorre amortecimento crítico em um sistema, quando o seu fator de amortecimento ξ , é exatamente igual a 1 :

E para nossa alegria o fator de amortecimento está relacionado ao coeficiente de amortecimento viscoso c pela seguinte fórmula:

ξ = c 2 m ω n

Sabendo que ξ = 1 e conhecendo os valores da outras variáveis, alcançamos nosso resultado:

1 = c 2 ( 35   k g ) ( 29,277   r a d / s )

c ≅ 2 ( 35   k g ) ( 29,277   r a d / s )

c ≅ 2050   N ⋅ s m

Resposta

c ≅ 2050   N ⋅ s m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um oscilador criticamente amortecido, partindo da posição de equilíbrio, recebe um impulso que lhe comunica uma velocidade inicial v 0 . Verifica-se que ele passa por seu deslocamento máximo, igual a
Seja r a razão entre dois máximos consecutivos do deslocamento de um oscilador livre fracamente amortecido ( γ ≪ ω 0 ). O parâmeto δ = ln ⁡ r chama-se decremento logarítmico. (a) Relacione δ com a con
Verifique que x 1 t = t e - γ 2 t é solução da x ¨ + γ x ˙ + ω 0 2 x = 0 para ω 0 = γ / 2 , e que a x t = F 0 2 m ω 0 t sen ⁡ ω 0 t satisfaz a equação diferencial x ¨ + ω 0 2 x = F 0 m cos ⁡ ω 0 t e a
Um bloco cúbico de 10c m de aresta e densidade 8g / c m 3 está suspenso do teto por uma mola de constante elástica 40N / m e comprimento relaxado de 0,5m , e mergulhado dentro de um fluido viscoso de
Uma partícula de massa m move-se na direção z no interior de um fluido, cuja resistência de atrito é da forma - ρ z ˙ ou seja, é proporcional à velocidade ρ0 . A força peso é desprezível em confronto