Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 83

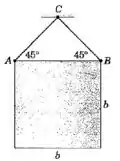
O painel quadrado uniforme de 12   k g está suspenso a partir do ponto C pelos dois fios presos em A e B . Se o fio em B de repente se rompe, calcule a tração T no fio em A logo após a ruptura ocorrer.

Passo 1

Vamos calcular a soma dos momentos em relação ao ponto A , no instante imediatamente após a ruptura do fio em B :

∑ M A = I α + m a - d

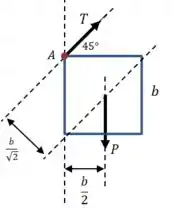
E o momento da força peso em relação ao ponto A é:

∑ M A = P b 2 = m g b 2

O momento de inércia do quadrado em relação ao seu centro de massa é:

I = 1 6 m b 2

E a aceleração a - do centro de massa pode ser escrita em função da aceleração angular e da distância d = b 2 :

m a - d = m d α d = m d 2 α

m g b 2 = 1 6 m b 2 + m b 2 2 α

g b 2 = b 2 6 + b 2 2 α

α = g 2 b 1 6 + 1 2 = 3 g 4 b

Passo 2

E para encontrar a tração T , vamos considerar a soma dos momentos em relação ao centro de massa:

∑ M G = I α

Olhando o desenho, podemos escrever o momento da tração T em relação ao centro de massa da seguinte forma:

∑ M G = T b 2

E então:

T b 2 = 1 6 m b 2   3 g 4 b

T = 3 2 24 m g = 3 2 24 12 9,81

T = 20,8   N

Resposta

A tração no fio é T = 20,8   N nesse instante.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um estudo da lesão na cabeça contra o painel de instrumentos de um carro durante paradas bruscas ou em colisões onde cintos de segurança abdominais, sem alça no ombro, ou airbags são utilizados, o
Duas rodas em formato de disco, cada uma com massa m , estão ligadas por uma barra leve, porém rígida de comrpimento l . O conjunto é arremessado de uma superfície horizontal, com velocidade v conform
Determine a força horizontal máxima P que pode ser aplicada ao carrinho de massa M para que a roda não deslize quando começar a rolar sobre o carrinho. A roda tem massa m , raio r e raio de giração k
O cilindro hidráulico B C do caminhão basculante está quebrado e desconectado. O motorista (que fez curso de dinâmica) decide calcular a aceleração mínima a do caminhão necessária para inclinar o depó
Uma bola de boliche de 6,4k g com uma circunferência de 690m m tem um raio de giração de 83m m . Se a bola é lançada com uma velocidade de 6m / s , mas sem velocidade angular quando toca o chão da pis