Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 85
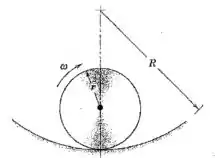
O disco circular de massa e raio está rolando na parte mais baixa da trajetória circular de raio . Se o disco possui uma velocidade angular , determine a força exercida pela trajetória sobre o disco.
Passo 1
Conforme o disco rola pela trajetória de raio , o centro de massa do disco descreve uma trajetória de raio .
Portanto, para que o centro de massa mantenha essa trajetória com velocidade linear , ele deve possuir uma aceleração centrípeta :
E como o disco gira com velocidade angular e tem raio , a sua velocidade linear é:
Então:
Passo 2
E então podemos utilizar a segunda lei de Newton na direção centrípeta:
As forças que agem nessa direção são a força normal da trajetória sobre o disco e a força peso:
Resposta
A força normal é .
Exercícios de Livros Relacionados
O caminhão, inicialmente em repouso com um rolo de papel cilíndrico compacto na posição mostrada, se desloca para a frente com uma aceleração constante a . Encontre a distância s que o caminhão percor
A extremidade A da barra uniforme de 5k g é livremente articulada no cursor, que possui uma aceleração a = 4 m / s 2 ao longo do eixo horizontal fixo. Se a barra tem uma velocidade angular no sentido
O haste esbelta de massa m e comprimento l é liberada a partir do repouso na posição vertical com o pequeno rolete na extremidade a apoiado sobre o plano inclinado. Determine a aceleração inicial de A
A casca semicilíndrica uniforme de massa m e raio r é liberada a partir do repouso na posição mostra, com sua borda inferior apoiada sobre a superfície horizontal. Determine o coeficiente de atrito es
Pequenos roletes sobre rolamentos montados nas extremidades da barra esbelta de massa m e comprimento l limitam o movimento da barra nas ranhuras horizontais x - y . Se um momento M é aplicado à barra