Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 80
Repita o Prob. 6/79, exceto que , e .
Imagem do Prob. 6/79:
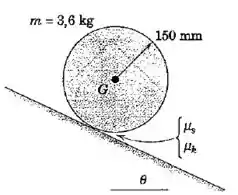
Passo 1
Inicialmente, podemos simplesmente refazer os cálculos do problema anterior:
O diagrama das forças que agem sobre o cilindro fica da seguinte forma:
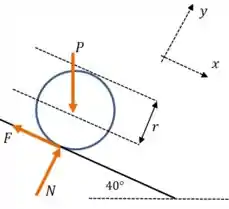
E então podemos aplicar a segunda lei de Newton em cada direção:
E podemos escrever também uma equação para os momentos em relação ao centro do cilindro:
Passo 2
E assim ficamos com um sistema de quatro equações e quatro variáveis desconhecidas:
Onde a primeira equação parte da suposição de que o cilindro rola sem deslizar, algo que precisaremos verificar depois.
Vamos substituir os valores numéricos:
E agora resolver para encontrar e . Substituindo a primeira equação na terceira:
E dividindo a segunda equação por dois temos o seguinte:
E pelo resultado anterior:
E substituindo no resultado anterior para encontrar :
Passo 3
Agora vamos verificar se o rolamento sem deslizamento realmente acontece. Como o coeficiente de atrito estático é , a força de atrito máxima que pode existir entre o cilindro e o plano é:
E podemos retornar ao sistema para encontrar a força normal:
E como esse valor é inferior ao que calculamos acima (), o cilindro vai deslizar, e a força terá o valor associado ao coeficiente de atrito cinético:
E agora retornamos à segunda equação do nosso sitema de antes (que continua válida):
Resposta
Nesse caso a força é e a aceleração é .