Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 4

O ‘pantógrafo de Nuremberg’ está sujeito a uma força horizontal P = 600 N. Determine a rigidez k para o equilíbrio quando θ=60º . A mola está livre quando θ=15º.

Passo 1

Desenhando o diagrama do corpo livre e o diagrama de deslocamentos virtuais:

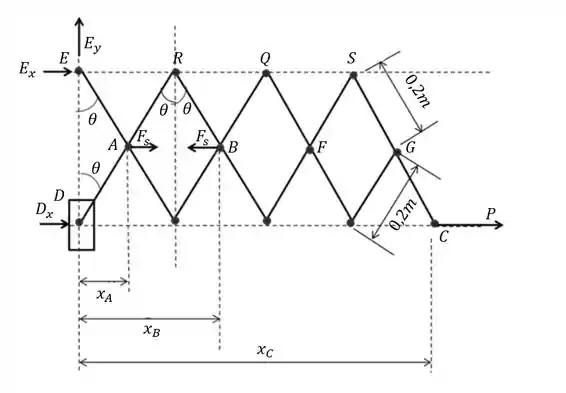
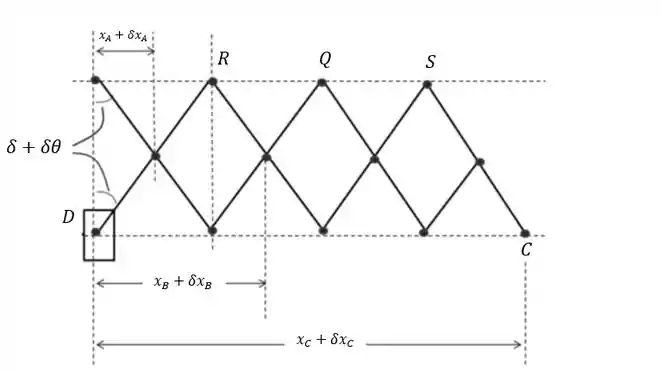
Passo 2

Do enunciado temos que o pantógrafo está sujeito a uma força horizontal P = 600   N e existe uma mola conectada entre A e B.

Dados:   θ 0 = 15 º

Passo 3

O próximo passo é definicar as coordenadas x A , x B e x C em milímetros tomando como referencia o eixo y (ED):

Como EA=ED, o ângulo EDA também é θ:

x A = 200 ⋅ sen ⁡ θ x B = 3 × 200 ⋅ sen ⁡ θ = 600 ⋅ sen ⁡ θ x C = 8 × 200 × s e n θ = 1600 ⋅ sen ⁡ θ

Nessa parte, observar o desenho. Atentar pras distâncias em MILÍMETROS

Achando os deslocamentos virtuais, derivando-se cada expressão temos:

δ x A = 200 ⋅ cos ⁡ θ δ ⋅ δ θ δ x B = 600 ⋅ cos ⁡ θ δ ⋅ δ θ δ x C = 1600 ⋅ cos ⁡ θ δ ⋅ δ θ

Passo 4

Agora vamos calcular a distância entre A e B:

x A B = ( 600 - 400 ) ⋅ sen ⁡ θ = 200 ⋅ sen ⁡ θ

O enlongamento da mola na posição inicial é :

s = x A B θ - x A B θ = 15 º s = 400 ⋅ sen ⁡ θ - 400 ⋅ sen ⁡ 15 º s = 400 ⋅ sen ⁡ θ   - 103,53

Passo 5

Aplicando a lei de Hooke, a força da mola pode ser dada por:

F S = k ⋅ s = k ⋅ ( 400 sen ⁡ θ - 103,53 )

Passo 6

Com todos os dados, podemos enfim calcular o trabalho virtual:

δ U = 0 F s ⋅ 200 ⋅ cos ⁡ θ δ ⋅ δ θ - F s ⋅ 600 ⋅ cos ⁡ θ δ ⋅ δ θ + P ⋅ 1600 ⋅ cos ⁡ θ δ ⋅ δ θ = 0 - 400 ⋅ F s ⋅ cos ⁡ θ δ ⋅ δ θ = - P ⋅ 1600 ⋅ cos ⁡ θ δ ⋅ δ θ - 400 ⋅ F s = - P ⋅ 1600 4 P = F s

Passo 7

Substituindo o valor de F s e θ :

4 P = F s

k ⋅ ( 400 sen ⁡ 60 º - 103,53 ) = 4 × 600 k ⋅ ( 400 sen ⁡ 60 º - 103,53 ) = 4 × 600 k = 4 × 600   400 sen ⁡ 60 º - 103,53     = 9,88 N m m = 9,88 k N m

Resposta

k = 9,88 k N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma extremidade da mola de torção é fixada ao solo em A e a outra extremidade é fixada ao eixo em B. A rigidez torcional K da mola elástica é o torque necessário para torcer a mola em um ângulo de um
Determine a altura máxima h da massa m para a qual o pêndulo invertido será estável na posição vertical mostrada. Cada uma das molas tem uma rigidez k, e elas têm pré-compressão iguais nesta posição.
O pêndulo de 3 lb oscila em torno do eixo OO e tem um centro de massa em G. Quando θ = 0, cada mola tem um alongamento inicial de 4 pol. Calcule a rigidez máxima k de cada uma das molas paralelas que
O pêndulo invertido de massa me centro de massa G é sustentado pelas duas molas, cada uma de rigidez k. Se as molas estiverem igualmente esticadas quando o pêndulo estiver na posição vertical mostrada
A seção transversal de um alçapão articulado em A e tendo uma massa me um centro de massa em G é mostrado na figura. A mola é comprimida pela haste que é fixada na extremidade inferior da porta e que