Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 81
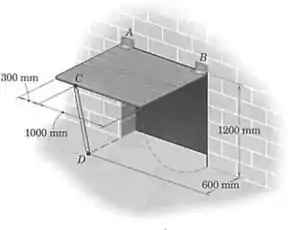
A porta retangular de acesso com é mantida na posição aberta, a , pelo apoio simples . Determine a força no apoio e o módulo da força normal ao eixo de abertura em cada uma das duas pequenas dobradiças e .
Passo 1
Primeiro precisamos definir um sistema de coordenadas e desenhar as forças envolvidas:
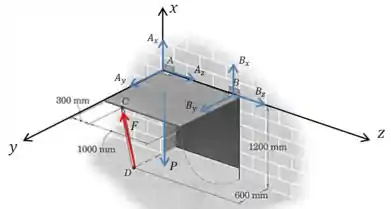
E nosso objetivo é encontrar o módulo das forças normais ao eixo em e (ou seja, apenas as componentes , , e ) e da força no apoio.
Como a força não é paralela a nenhum eixo, seria útil escrever sua forma vetorial antes de começarmos a resolver a questão:
Onde é o vetor unitário na direção :
Ok, isso vai ajudar bastante nos próximos passos.
Passo 2
Vamos começar com algumas equações de equilíbrio, temos que calcular os momentos em relação ao três eixos.
Para o eixo , todas as forças em e têm momento nulo, já que o eixo passa por esses dois pontos, e ficamos apenas com os momentos de e (e apenas a componente de produz momento nesse caso):
Quando consideramos o eixo vamos nos livrar de todas as forças que agem em , das componentes e da força , e das componentes e da força .
Então ficamos apenas com o peso , e as componentes e :
Já podemos substituir os valores para encontrar :
E agora só fica faltando o momento em relação ao eixo . Nesse caso, as únicas forças que produzem momento são e :
Passo 3
E com as informações que temos já podemos calcular o módulo da força normal ao eixo em :
Mas ainda falta encontrar as componentes e da força . Vamos tentar fazer isso usando a condição de equilíbrio das forças:
E agora vamos fazer a mesma coisa para a direção do eixo :
Agora sim, já podemos calcular o módulo da força normal ao eixo em :
Resposta
Os módulos das forças são , e .