Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 90
A mola de módulo é esticada de uma distância quando o mecanismo está na posição mostrada. Calcule a força necessária para iniciar rotação em torno do eixo e determine os módulos correspondentes das forças nos mancais, as quas são perpendiculares à . Qual é a força de reação normal em se ?
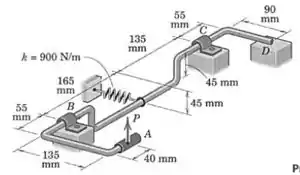
Passo 1
Vamos começar definindo um sistema de eixos e desenhando as forças que atuam sobre o sistema:
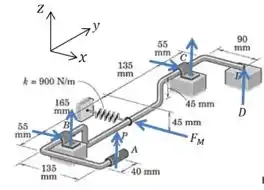
Não colocamos legenda em todos os vetores para evitar poluição no desenho, mas as setas nos pontos e indicam as componentes , , e das forças que queremos calcular.
Como estamos lidando com o momento em que o sistema inicia a rotação, podemos considerar que , já que está prestes a haver perda de contato naquele ponto.
Passo 2
Vamos escrever equações de equilíbrio que nos ajudem a resolver o problema. Quando tratamos do equilíbrio dos momentos, isso basicamente significa que temos que escolher os eixos de forma inteligente.
Quando escolhemos um eixo que passa por cima ou é paralelo à linha de ação de algumas forças elas desaparecem da equação, e assim nós encontramos expressões para as forças que restaram.
Por exemplo, vamos ver a condição de equilíbrio para o momento em relação ao eixo . Nesse caso todas as forças em e têm momento nulo:
Agora vamos escolher vários outros eixos, de forma que em cada caso nós anulemos algumas forças, mas não outras.
O momento na direção da força vai deixar apenas e :
O momento na direção da força vai deixar apenas e :
Passo 3
Agora vamos ver o que podemos tirar desse sistema:
A força na mola pode ser calculada com as informações do enunciado:
Então a primeira equação dá:
Que é justamente o que estávamos procurando, já que estamos analisando o caso em que o movimento está prestes a começar.
Substituindo isso na segunda:
E substituindo o valor de na terceira:
Passo 4
Agora vamos usar a condição de equilíbrio das forças.
Primeira na direção do eixo :
E agora na direção do eixo :
E agora podemos calcular os módulos das duas forças:
Passo 5
E a última tarefa é encontrar a força em no caso em que:
Agora que já temos todas as forças, podemos escolher um eixo com grande tranquilidade. Vamos voltar ao momento em relação ao eixo :
Simplesmente adicionamos o termo com o momento de na equação que já tínhamos. Agora vamos substituir os valores numéricos:
Resposta
As forças são , e . No caso em que o valor da força em é .