Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 187
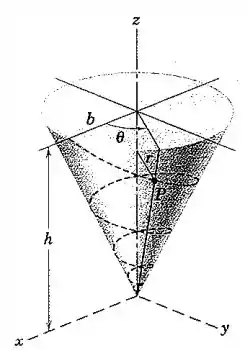
A partícula se desloca para baixo na trajetória espiral que está enrolada ao redor da superfície de um cone circular reto com raio de base e altura . O ângulo entre a tangente à curva em qualquer ponto e uma tangente horizontal ao cone neste ponto é constante. Além disso, o movimento da partícula é controlado de modo que é constante. Determine a expressão para a aceleração radial da partícula para qualquer valor de .
Passo 1
Olhando para um determinado ponto da trajetória da partícula, traçamos uma distância infinitesimal na direção da trajetória (ao longo da curva espiral) e a distância infinitesimal correspondente na direção da geratriz do cone, olha só:
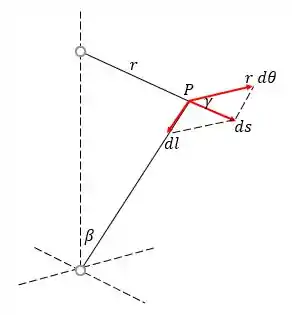
Pela figura, obtemos duas equações relacionando essas distâncias:
Ou seja,
Passo 2
Show! Agora vamos integrar cada lado da equação anterior, lembrando que quando , a partícula está no topo do cone, e aí :
onde .
Veja também que pode ser calculado por meio das medidas da base e da altura do cone:
Passo 3
Agora, lembre-se de que a aceleração radial é dada pela fórmula:
Já sabemos que:
Para encontrar , podemos derivar essa equação duas vezes, certo?
Na segunda derivação, utilizamos a regra do produto. E repare que , pois o enunciado diz que é constante. Então:
Logo,
Resposta
com