Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 190
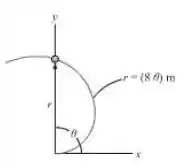
Uma partícula move-se ao longo de uma espiral de Arquimedes , onde é dado em radianos. Se (constante), determine as componentes radiais e transversais da velocidade e aceleração da partícula no instante que . Trace a curva e mostre as componentes na curva.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vamos primeiro fazer as contas para ai sabermos as direções das componentes radiais e transversais da aceleração e velocidade.
Do enunciado, temos que é constante, portanto:
Quando , temos:
Temos também que:
E:
Passo 2
Sabemos que:
Passo 3
Para a aceleração, teremos que a componente é:
A componente é dada por:
Passo 4
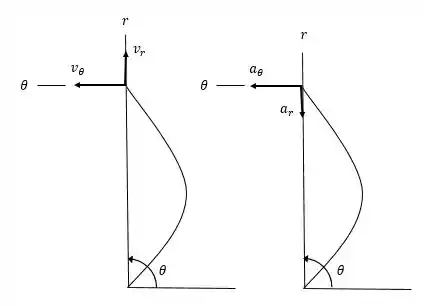
As componentes estão então retratadas nos diagramas abaixo:
Resposta
Exercícios de Livros Relacionados
2/122) O projeto de um sistema de comando de válvulas de um motor de autonóvel de quatro cilindors é mostrado. Quando o motor é acelerado , a velocidade da correia v varia uniformemente de 3 m / s até
2/119) Um foguete viajando acima da atmosfera a uma altitude de 500k m teria uma aceleração em queda livre g = 8,43 m / s 2 na ausência de outras forças que não a atração gravitacional . Devido ao emp
2/123) Adireção do movimento de uma fita plana em um dispositivo de controle numérico é alterada pelas duas polias A e B mostradas . Se a velocidade da fita aumenta uniformemente a partir de 2 m / s a
2/125) Uma fita magnética corre sobre a polia louca em um computador conforme mostrado . Se aceleração total de um ponto P sobre a fita em contato com a polia faz um ângulo de 4 ° com a tangente á fit
2/127) Para a bola de beisebol do Prob. 2/126 , determine o raio de curvatura ρ da trajetória e a taxa de variação no tempo v ' da nos instantes t = 1s e t = 2,5s onde t = 0 é o instante do lançamento