Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 126
2/126) Um jogador de beisebol lança uma bola com as condições iniciais mostradas na figura . Determine o raio de curvatura da trajetória (a) logo após o lançamento e (b) no ápice . Para cada caso , calcule a taxa de variação no tempo da velocidade .
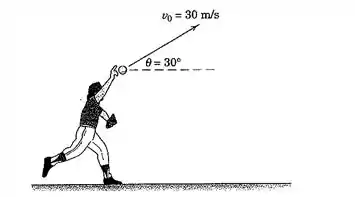
Passo 1
Bom pessoal , analisando a situação do problema , temos que :
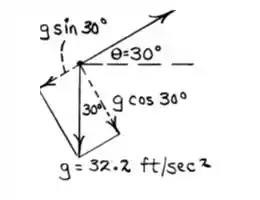
Dessa forma , podemos obter o raio de curvatura e a taxa de variação da velocidade no tempo simplesmente aplicando as relações :
Passo 2
Ao refazermos as operações anteriores no momento em que a bola atinge seu ápice , obtemos que :
Resposta
Respectivamente :
Exercícios de Livros Relacionados
2/150) Um projétil é lançado a partir do ponto Acom as condições iniciais mostradas . Co m as definições convencionais das coordenadas r e θ em relação ao sistema de coordenadas O x y , determine r ,
2/166) O robô de pinstura é programada para pintar uma linha de produção de superfícies curvas A( vista da borda ) . Ocomprimento do braço telescópico é controlado de acordo com b = 0,3 sen π t 2 ,
2/164) O pequeno bloco P parte do repouso no instante t = 0 no ponto A e sobe o plano inclinado com aceleração constante a . Determine r ' como uma função do tempo .
2/155) O cursor P pode ser deslocado para dentro por meio da corda S enquanto a barra AO gira em torno do pivôO . A posição angular da barra é dada por θ = 0,4 + 0,12 t + 0,06 t 3 , onde θ é em radian
2/158) Num determinado instante , uma partícula tem as seguintes componentes de posição , velocidade , e aceleração em relação a um sistema fixo de coordenadas x - y : x = 4 m , y = 2 m , x ' = 2 3m /