Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 118

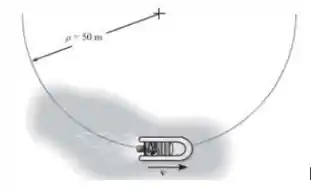
Partindo do repouso, uma lancha move-se em torno de uma trajetória circular, ρ = 50   m , a uma velocidade escalar v = 0,2   t 2   m / s , onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da lancha no instante t = 3   s .

Passo 1

A questão é mais fácil do que parece! Para determinar a intensidade da aceleração, basta fazer uma substituição direta t = 3 na função da velocidade! Simples né?! Já para determinarmos a aceleração, precisamos determinar ambas as componentes tangencial e normal. Para isto, utilizaremos as seguintes relações:

a n = v 2 ρ

a t = d v d t

Bem simples! Agora, só irmos direto para os cálculos!

Passo 2

Para determinarmos o valor da velocidade, vamos substituir o valor t = 3 na equação da velocidade. Desta forma,

v = 0,2 t 2

v = 0,2 ⋅ 3 2 = 1,8   m / s

Passo 3

Agora que determinarmos a velocidade, podemos calcular a componente normal da aceleração. Começando por ela então, temos:

a n = v 2 ρ = 1,8 2 50 = 0,0648   m / s 2

Já a componente tangencial é dada por:

a t = d v d t = 0,4   t

a t = 1,2   m / s

Passo 4

Após determinarmos ambas as componentes da aceleração, vamos calcular a sua intensidade! Sendo assim,

a = a t 2 + a n 2

a = 1,2   m / s 2

Resposta

v = 1,8   m / s

a = 1,2   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Foi observado que durante o primeiro sobrevoo da Terra feito pela espaçonave Galileu, sua altitude mínima foi de 960 km acima da superfície da Terra. Considerando que a trajetória da espaçonave era pa
Foi observado que durante o seu segundo sobrevoo da Terra, a espaçonave Galileu tinha uma velocidade de 14 × 10 ³ ³ m/s quando atingiu sua altitude mínima de 300 km acima da superfície da Terra. Deter
Para o Problema mostre que F é proporcional à distância r da partícula ao centro de força O.
Um satélite descreve uma trajetória elíptica em torno de um planetade massa M. Representando por r 0 e r 1 , respectivamente, os valoresmínimo e máximo da distância r do satélite ao centro do planeta,
Quando uma sonda espacial, que se aproxima do planeta Vênus em uma trajetória parabólica, atinge o ponto A mais próximo do planeta, sua velocidade é diminuída para que ela seja inserida em uma órbita