Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 63
A barra AB, de 500 g, está em repouso ao longo da superfície interna lisa de uma tigela hemisférica. Se a barra é liberada do repouso a partir da posição mostrada, determine sua velocidade angular no instante em que ela oscila para baixo e torna-se horizontal.
Passo 1
Iremos considerar a aceleração da gravidade
Para resolver esse exercício, iremos considerar o eixo de referência no fundo da tigela conforme figura 1:
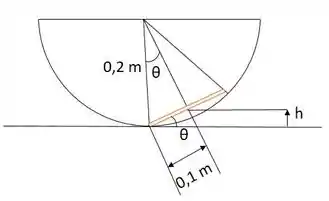
Sendo assim, o ângulo é dado por:
Podemos agora determinar o valor da altura h:
Passo 2
Agora, analisando a figura 2, podemos encontrar os valores dos segmentos CE e ED.
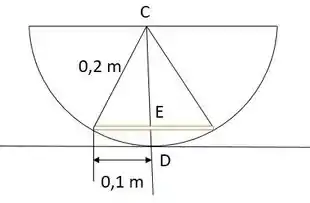
Dessa forma:
Passo 3
Com isso, podemos agora aplicar a equação da conservação da energia mecânica para encontrar a velocidade angular da barra AB:
Resposta
Exercícios de Livros Relacionados
O anel de 5 kg desliza ao longo da barra vertical lisa. Se o anel é tirado do repouso em A, determine a sua velocidade quando ele passa pelo ponto B. A mola tem um comprimento não deformado de 200 mm.
O bloco A de 15 kg é colocado sobre o topo de duas molas alinhadas, B e C, e, em seguida, é empurrado para baixo na posição mostrada. Se ele é solto em seguida, determine a sua altura máxima h que ele
A bola de massa m é submetida a uma velocidade de v A = 3 g r na posição A. Quando ela chega a B , o cabo atinge o pino P, após o que a bola descreve uma trajetória circular menor. Determine a posição
A bola de 0,5 kg é disparada pelo dispositivo com mola. A mola tem uma rigidez k = 400 N/m e os quatro cabos C e a placa P mantêm a mola comprimida 50 mm quando não há nenhuma carga sobre a placa. A p
O carrinho de montanha-russa e seus passageiros têm massa total m. Determine a menor velocidade que ele tem de ter quando entra no loop A de maneira que ele possa completar a volta sem deixar os trilh