Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 117
Partindo do repouso, uma lancha desloca-se ao longo da trajetória circular , a uma velocidade escalar , onde é dado em segundos. Determine as intensidades da velocidade e aceleração da lancha no instante em que .
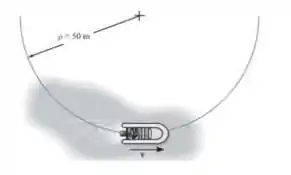
Passo 1
Fala pessoal, vamos começar com o pé direito resolvendo essa questão aqui?
Para podermos responder está questão, precisamos determinar qual o tempo em que o barco percorre uma distância de . Para isto, precisamos obter inicialmente a função posição do carro. Desta forma, precisamos resolver as seguintes integrais:
E resolvermos a equação acima pra . Após determinarmos o tempo, poderemos voltar e calcular a intensidade da velocidade, as componentes da aceleração e por fim determinar a sua intensidade!
Passo 2
Vamos começar resolvendo as integrais! Como e , pois o barco saiu da origem, para a posição, temos:
Substituindo :
Portanto, o tempo em que é:
Passo 3
Agora que determinamos o tempo , vamos calcular a intensidade da velocidade. Substituindo este valor da função velocidade, temos:
Passo 4
Agora, vamos fazer o mesmo para as componentes da aceleração. Começando pela componente normal, temos:
Já a componente tangencial é dada por:
Após determinarmos ambas as componentes da aceleração, vamos calcular a sua intensidade! Sendo assim,