Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 5

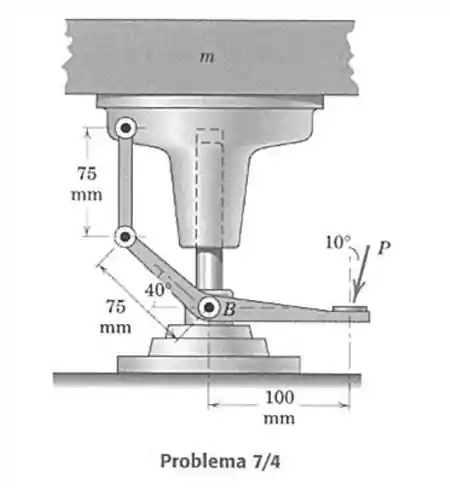
  1. O pedal é usado para levantar uma plataforma de massa m . Determine a força P necessária, aplicada em um ângulo de 10 ° , para suportar a carga de 80   k g .

Passo 1

Mais fácil fazer essa análise por momento em torno do ponto B , porém para reforçar os conhecimentos vamos compreender o sentido do movimento causado por essas forças.

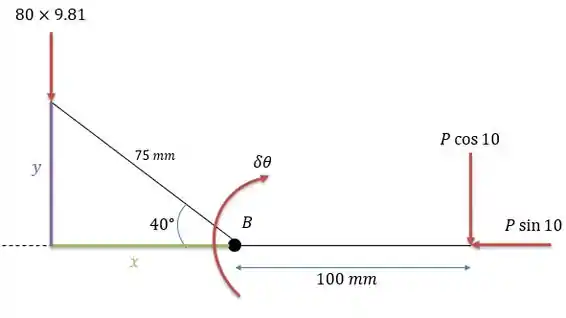
A força P pode ser rebatida em x para P s i n   10 com seu sentido indo para a esquerda e em y sendo igual a P c o s   10 com seu sentido para baixo.

A força P s i n   10 nos gera um deslocamento virtual em nenhum sentido de δ θ logo não gerará trabalho (para esse tipo de análise). Já a força P cos ⁡ 10 gera um deslocamento no eixo de 100   m m no sentido positivo de δ θ , logo será:

δ U P = 100 × 10 - 3 × P c o s   10

A força peso gera um deslocamento virtual no sentido δ θ no eixo x não em y . O valor de x pode ser calculado.

cos ⁡ 40 = x 75 × 10 - 3 → x = 75 × 10 - 3 × cos ⁡ 40

Em x essa força peso gerara um movimento no sentido horário, contrário ao sentido de δ θ , o que nos dá um trabalho virtual igual a:

δ U w = - 80 × 9.81 × x = - 784.8 × 75 × 10 - 3 cos ⁡ 40 = - 58.86 cos ⁡ 40

Passo 2

Logo a somatória dos trabalhos virtuais do sistemas será:

δ U w + δ U p = 100 × 10 - 3 × P c o s   10 - 58 . 8 6 cos ⁡ 40 = 0

Encontrando o valor de P temos:

P = 58.8 6 cos ⁡ 40 100 × 10 - 3 cos ⁡ 10 = 457.85   N

Resposta

P = 457.85   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força W de intensidade de 600 N é aplicada ao mecanismo articulado em B. A constante da mola é de k = 2.5k N / m , e a mola está indeformada quando AB e BC são horizontais. Desprezando o peso do m
Duas hastes AC e CE são unidas por um pino em C e por uma mola AE. A constante da mola é k, e a mola está indeformada quando θ = 30 ° . Para o carregamento mostrado na figura, deduza uma equação em P,
Uma alavanca AB é presa ao eixo horizontal BC que passa atravpes de uma mancal e é soldado a um suporte fixo em C. A constante de mola torcional do eixo BC é K, ou seja, é necessário um binário de int
A força P de intensidade 240 N é aplicada na ponta E do cabo CDE que passa por uma polia D e é fixado ao mecanismo em C. Desprezando o peso do mecanismo e o raio da polia, determine o valor de θ corre
A posição da manivela ABC é controlada pelo cilindro hidráulico BD. Para o carregamento mostrado na figura, (a) expresse a força exercido pelo cilindro hidráulico no pino B em função do comprimento BD