Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 6

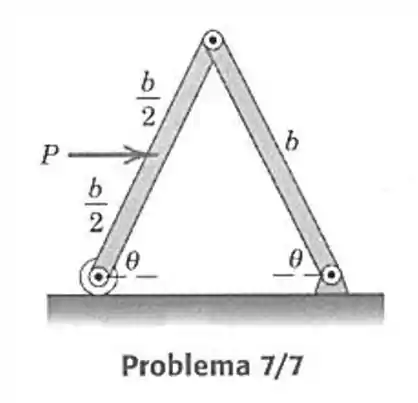
  1. Substitua o binário M do Prob. 7/6 pela força horizontal P . Como mostrado, e determine o ângulo de equilíbrio θ .

Passo 1

Traçando os eixos pertinentes para resolver esse problema nós teremos o seguinte esquema:

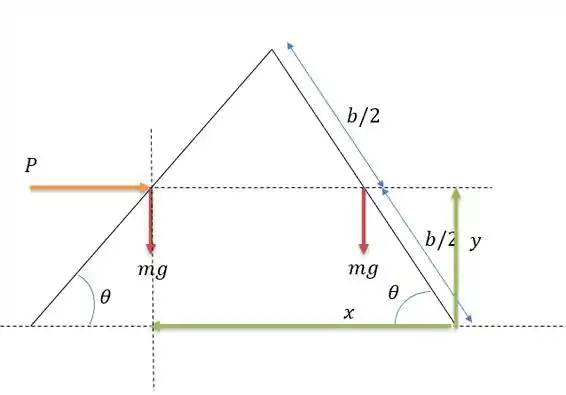
Onde os eixos x e y devem começar na estrutura e terminar na força, logo aplicando a teoria de trabalhos virtuais nós teremos:

δ U = - P δ x - 2 m g δ y - m g   δ y = 0

Onde P tende a diminuir o valor o tamanho da reta de tamanho x e as forças peso das barras tendem a diminuir o tamanho da reta de tamanho y .

Passo 2

A geometria do problema nos dá os seguintes valores de x e y .

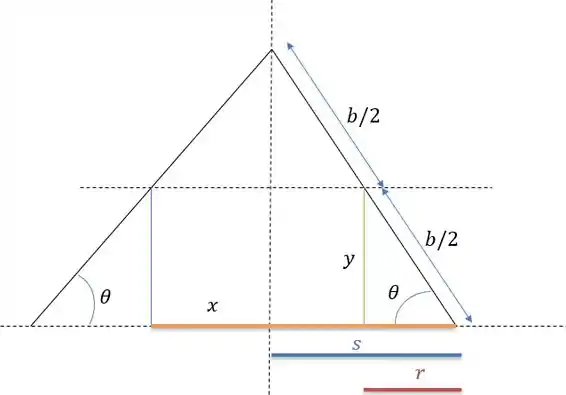
Onde o valor de y é encontrado pelo triângulo retângulo menor formado pelos catetos y e r . E que será calculado por:

sin ⁡ θ = y b 2 → y = b 2 sin ⁡ θ

E o valor de x pode ser calculada pela soma de valores das retas de s e r .

x = s + r

s se calcula pelo triângulo retângulo maior.

cos ⁡ θ = s b → s = b c o s   θ

E r pelo menor.

cos ⁡ θ = r b 2 → r = b 2 cos ⁡ θ

Logo x   será:

x = b cos ⁡ θ + b 2 cos ⁡ θ = 3 b 2 cos ⁡ θ

Passo 3

Aplicando esses valores na equação do somatório de trabalhos virtuais:

- P   δ 3 b 2 cos ⁡ θ - 2 m g   δ b 2 sin ⁡ θ = 0

Fazendo essa derivada:

- P × - 3 b 2 sin ⁡ θ   δ θ - 2 m g b 2 cos ⁡ θ = 0

3 P b 2 sin ⁡ θ = 2 m g b 2 cos ⁡ θ

t g   θ = 2 m g 3 P

θ = t g - 1 2 m g 3 P

Resposta

θ = t g - 1 2 m g 3 P

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força vertical P que deve ser aplicada em C para se manter o equilíbrio do sistema articulado.
9. Sabendo que a linha de ação da força Q passa pelo ponto C , deduza uma expressão para a intensidade de Q necessária para se manter o equilíbrio.
11. A força P atua sobre o mecanismo mostrado na figura. Deduza uma expressão para a intensidade da força Q necessária para o equilíbrio.
13. A haste fina A B é presa a um colar A e repousa sobre uma pequena roda em C . Desprezando o raio da roda e o efeito do atrito, deduza uma expressão para a intensidade da força Q necessária para se
15. Uma barra uniforme A B de comprimento l e peso W é suspenso por duas cordas A C e B C de igual comprimento. Deduza uma expressão para a intensidade do binário M necessária para manter o equilíbrio