Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 239

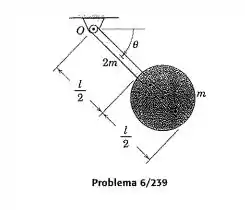
O pêndulo composto é constituído de uma haste esbelta uniforme de comprimento l e massa 2 ⋅ m à qual está fixado um disco uniforme de diâmetro l / 2   e massa m . O corpo gira livremente em torno de um eixo horizontal através de O . Se o pêndulo tem uma velocidade angular no sentido horário de 3 rad/s quando θ = 0 no instante de tempo t = 0 , determine o tempo t no qual o pêndulo passa pela posição θ = 90 º . O comprimento do pendulo l = 0.8   m .

Passo 1

Para resolvermos esse problema, iremos precisar calcular a posição do centro de massa do sistema e seu momento de inércia. Após isso vamos aplicar a relação de torque para encontrarmos uma equação para o tempo.

Passo 2

Vamos iniciar encontrando a posição do centro de massa. Sabemos que a mesma pode ser encontrada pela relação

r c m = ∑ m ⋅ r c m o b j M = 2 ⋅ m ⋅ l 2 + m ⋅ 3 ⋅ l 4 3 ⋅ m = 7 12 ⋅ l

Onde r c m o b j é a posição do centro de massa de cada objeto que compõem o sistema. Calculando agora o momento de inércia, temos que ele será dado pela soma dos momentos de inércia de cada objeto do sistema. Temos então que

I o = I b a r r a + I d i s c o = 1 3 ⋅ m b a r r a ⋅ L b a r r a 2 + 1 2 ⋅ m ⋅ R 2 + m ⋅ R + L c d 2

Onde L c d é a distância até o centro do disco. Substituindo os valores, chegamos que o momento de inércia total é

I o = 121 96 ⋅ m ⋅ l 2

Temos também que o torque total exercido no centro de massa é dado pela força peso. Assim, temos que

F p e s o ⋅ r c m ⋅ sin ⁡ θ = τ = I o ⋅ α

3 ⋅ m ⋅ g ⋅ 7 12 ⋅ l ⋅ cos ⁡ θ = 121 96 ⋅ m ⋅ l 2 ⋅ α

α = 168 121 ⋅ g l ⋅ cos ⁡ θ

Agora que encontramos α podemos criar uma relação com a velocidade angular ω para obtermos o tempo. Temos que a aceleração angular pode ser dada por

α = d ω d t = d θ d t ⋅ d ω d θ = ω ⋅ d ω d θ

ω ⋅ d ω d θ = 168 121 ⋅ g l ⋅ cos ⁡ θ

ω ⋅ d ω = 168 121 ⋅ g l ⋅ cos ⁡ θ ⋅ d θ

∫ ω o ω ω ⋅ d ω = 168 121 ⋅ g l ⋅ ∫ 0 θ cos ⁡ θ ⋅ d θ

ω = ω o 2 + 336 121 ⋅ g l ⋅ sin ⁡ θ = d θ d t

Fazendo o mesmo procedimento, chegamos na seguinte integral para o tempo

t = ∫ 0 θ d θ ω o 2 + 336 121 ⋅ g l ⋅ sin ⁡ θ

Com os dados mostrados no problema e resolvendo com o auxílio de um programa, teremos que t = 0.302   s

Resposta

t = 0.302   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante que r = 1,5m , ao disco de 5k g é dada uma velocidade v = 5 m / s , perpendicular à corda elástica. Determine a velocidade do disco e a taxa de encurtamento da corda elástica no instante r
A bola de 2k g gira em torno de uma trajetória circular de 0,5m de diâmetro com velocidade constante. Se o comprimento da corda é encurtado de l = 1m até l ' = 0,5m , puxando-se a corda através do tub
Quando se dá ao pêndulo de 2k g uma velocidade horizontal de 1,5m / s , ele começa a girar em torno da trajetória circular horizontal A . Se a força F na corda é aumentada, o pêndulo sobe, e então gir
O barco-bombeiro descarrega dois jatos de água do mar, cada um com vazão de 0,25m 3 / s a uma velocidade de saída de 50m / s . Determine a tração desenvolvida na corrente da âncora, necessária para se
O ventilador sopra o ar a 162m 3 / m i n . Se o ventilador pesa 150N( m ≈ 15k g ) e tem um centro de gravidade em G , determine o menor diâmetro d de sua base, necessário para que ele não tombe. O pes