Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 69

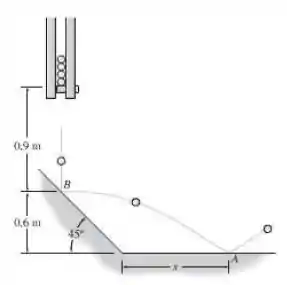
Para testar as propriedades de fabricação de bolas de aço de 1   k g , cada bola é liberada do repouso como mostrado e atinge a superfície lisa inclinada de 45 ° . Se o coeficiente de restituição é e = 0,8 , determine a distância S até onde a bola atinge o plano horizontal em A . Em que velocidade a bola atinge o ponto A ?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeiro vamos descobrir com que velocidade a bola chega no ponto B , para depois a partir da conservação de movimento, descobrirmos com que velocidade a bola sai de B , pois se soubermos essa velocidade, fica fácil pra descobrir o quanto a bolinha “andou” até chegar em A .

Aplicando conservação de energia, temos:

T 1 + V 1 = T 2 + V 2

1 2 m 1 v 1 2 + m g h 1 = 1 2 m v 2 2 + m g h 2

0 + ( 1 ) ( 9,81 ) ( 0,9 ) = 1 2 1 v B 1 2 + 0

v B 1 = 4,2   m / s

Bom... sabemos a velocidade de chegada da bola, agora vamos aplicar o principio da conservação da quantidade de movimento para determinar a velocidade de saída.

Como a bolinha sai com uma certa angulação, temos que descobrir as componentes dessa velocidade para depois descobri a magnitude. Vamos considerar nossos eixos como mostrado no diagrama abaixo:

↘ +       ∑ m v B x 1 = ∑ m v B x 2

1 4,2 sin ⁡ 45 ° = ( 1 ) v B 2 sin ⁡ θ

v B 2 sin ⁡ θ = 2,97   m / s

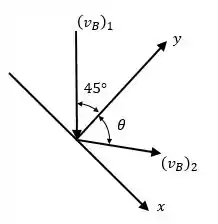
Para descobrir a componente em y , podemos usar:

↗ +       e = v B y 2 - 0 0 - v B y 1

0,8 = v B 2 cos ⁡ θ - 0 0 - - 4,2 cos ⁡ 45 °

v B 2 cos ⁡ θ = 2,376   m / s

A magnitude v B 2 será:

v B 2 = v B 2 cos ⁡ θ 2 + v B 2 sin ⁡ θ 2

v B 2 = 2,376 2 + 2,97 2

v B 2 = 3,8   m / s

A direção é dada por:

θ = tan - 1 ⁡ v B 2 sin ⁡ θ v B 2 cos ⁡ θ

θ = tan - 1 ⁡ 2,97 2,376  

θ = 51,34 °

Passo 2

Agora que temos esses dados, podemos facilmente encontrar a distância S . Vamos analisar o novo diagrama de corpo livre:

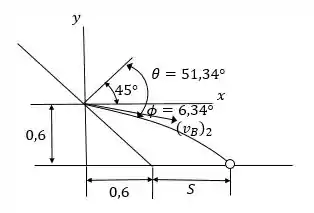
Consideraremos um ângulo ϕ para efeito de cálculo.

S + 0,6 = v B 2 cos ⁡ ϕ ⋅ t

Temos que encontrar o tempo do movimento:

↓ +       v 2 = v 0 2 + 2 a s - s 0

v A 2 y = 3,8 sin ⁡ 6,43 ° 2 + 2 ( 9,81 ) ( 0,6 - 0 )

v A y = 3,46   m / s  

v = v 0 + a t

3,46 = 3,8 sin ⁡ 6,34 ° + 9,81 t

t = 0,31   s

Portanto:

S + 0,6 = 3,8 cos ⁡ 6,34 ⋅ 0,31

S = 0,571   m

Temos também que:

v A x = 3,8 cos ⁡ 6,34

v A x = 3,78   m / s

A magnitude da velocidade de chegada em A é:

v A = v A x 2 + v A y 2

v A = 3,78   2 + 3,46 2

v A = 5,12   m / s

Resposta

S = 0,571   m

v A = 5,12   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco B de 4 kg está ligado ao eixo de um motor montado sobre a placa A, que pode girar livremente em torno do eixo vertical C. A unidade motor-placa-eixo tem um momento de inércia de 0,20 kg ∙ m2 e
Uma plataforma circular A é presa a um aro de raio interno de 200 mm e pode girar livremente sobre um eixo vertical. É sabido que a unidade plataforma-aro tem massa de 5 kg e raio de giração de 175 mm
Um pequeno cursor C de 2 kg pode deslizar livremente sobre um anel fino de massa de 3 kg e raio de 250 mm. O anel está soldado a um eixo vertical curto, que pode girar livremente em um mancal fixo. In
Um cursor C de 3 kg é preso a uma mola e pode deslizar na barra AB, podendo girar em torno do plano horizontal. O momento de inércia da massa da barra AB em relação a extremidade A é 0,5 kg ∙ m2. A mo
O cursor C tem massa de 8 kg e pode deslizar livremente sobre a barra AB, que por sua vez pode girar livremente em um plano horizontal. O conjunto está girando com uma velocidade angular ω de 1,5 rad/