Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 88

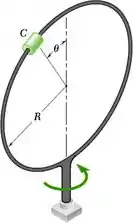
Um pequeno cursor C de 2 kg pode deslizar livremente sobre um anel fino de massa de 3 kg e raio de 250 mm. O anel está soldado a um eixo vertical curto, que pode girar livremente em um mancal fixo. Inicialmente, o anel tem uma velocidade angular de 35 rad/s e o cursor está no alto do anel ( θ = 0), quando este recebe um leve toque. Desprezando o efeito do atrito, determine (a) a velocidade angular do anel quando o cursor passar pela posição θ = 90°, (b) a velocidade correspondente do cursor relativamente ao anel.

Passo 1

O enunciado pede que a gente determine (a) a velocidade angular do anel quando o cursor passar pela posição θ = 90°, (b) a velocidade correspondente do cursor relativamente ao anel.

Momento de inércia do anel:

I - R = 1 2 m R R 2

Passo 2

Posição 1.

θ = 0

v C = 0

Posição 2.

θ = 90 °

v C y = v y = R ω 2

Passo 3

Conservação do momento angular em torno do eixo y para o sistema.

I - R ω 1 = I - R ω 2 + m C v y R

1 2 m R R 2 ω 1 = 1 2 m R R 2 ω 2 + m C R 2 ω 2

m R R 2 ω 1 = m R + 2 m C R 2 ω 2

ω 2 = m R m R + 2 m C ω 1

Passo 4

Energia potencial. Datum é o centro do anel.

V 1 = m C g R               V 2 = 0

Energia cinética:

T 1 = 1 2 I - R ω 1 2 1 2 m R R 2 ω 1 2 = 1 4 m R R 2 ω 1 2

T 1 = 1 2 I - R ω 1 2 1 2 m R R 2 ω 1 2 = 1 4 m R R 2 ω 2 2 + 1 2 m C R 2 v 2 2 + 1 2 m C v y 2

Passo 5

Princípio da conservação da energia

T 1 + V 1 = T 2 + V 2

1 4 m R R 2 ω 1 2 + m C g R = 1 4 m R + 1 2 m C R 2 ω 2 2 + 1 2 m C v y 2

Passo 6

Dados:

m C = 2   kg

m R = 3   kg

R = 0.25   m

ω 1 = 35   rad/s

Passo 7

  1. Velocidade angular.

    2. Da Eq. (1),

    ω 2 = 3   kg 3   kg + 2 2   kg

    ω 2 = 15.00   rad/s

    Passo 8

  2. Velocidade do colar em relação ao anel.

Da Eq. (2),

1 4 3   kg 0.25   m 2 35   rad/s 2 + 2   kg 9.81   m/ s 2 0.25   m

= 1 4 3   kg + 1 2 2   kg 0.25   m 2 15   rad/s 2 + 1 2 2   kg v y 2

57.422 + 4.905 = 24.609 + v y 2

v y 2 = 37.716

Resposta

a )   ω 2 = 15.00   rad/s

b )   v y = 6.14   m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco A, de massa de 2,5 kg e raio r = 100 mm, está em estado de repouso quando é posto em contato com uma esteira que se move à velocidade constante de v = 15 m/s. Sabendo que k = 0,20 entre o disc
Uma fita move-se sobre dois tambores mostrados na figura. O tambor A tem massa de 1,4 lb e raio de giração de 0,75 in, enquanto o tambor B tem massa de 3,5 lb e raio de giração de 1,25 in. Na porção i
A polia dupla mostrada tem uma massa de 3 kg e um raio de giração de 100 mm. Sabendo que quando a polia está em repouso, uma força P de magnitude 24 N é aplicada à corda B, determine (a) a velocidade
Dois cilindros uniformes, cada um com peso W = 14 lb e raio r = 5 pol. são conectados por uma correia, conforme mostrado. Se o sistema é liberado do repouso quando t = 0, determine (a) a velocidade do
Um volante é rigidamente preso a um eixo de 1,5 pol. de raio que rola sem deslizar ao longo dos trilhos paralelos. Sabendo que após ser liberado do repouso o sistema atinge uma velocidade de 6 em 30 s