Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 118

Os pesos dos vários componentes do caminhão são mostrados. Substitua esse sistema de forças por uma força resultante equivalente e especifique sua posição medida a partir do ponto B .

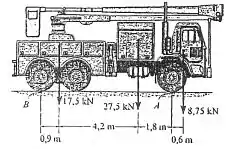
Passo 1

A questão pede para você substituir o sistema de forças que age sobre o caminhão por uma força resultante equivalente e indicar sua posição medida a partir do ponto B . Como se trata de um sistema de forças paralelas não precisamos adicionar um momento de binário equivalente: basta escolher o ponto correto de aplicação da resultante!

O primeiro passo é calcular a força resultante:

F R → = - 17,5 j ^   k N + - 27,5 j ^   k N + - 8,75 j ^   k N

Assim,

F R → = - 53,75 j ^   k N

Passo 2

Agora precisamos calcular os momentos de cada uma dessas forças com relação ao ponto B . Sabemos que o momento de uma força é dado por

M → = r → × F →

Desta forma,

M R → B = 0,9 i ^   m × - 17,5 j ^   k N + 5,1 i ^   m × - 27,5 j ^   k N + 7,5 i ^   m × - 8,75 j ^   k N

Portanto,

M R → B = - 15,75 - 140,25 - 65,625 k ^   k N ⋅ m

Logo,

M R → B = - 221,625 k ^   k N ⋅ m

Passo 3

Por fim, precisamos descobrir a que distância do ponto B deve ser aplicada a resultante para que o binário resultante não precise ser adicionado ao sistema:

d i ^ × - 53,75 j ^   k N = - 221,625 k ^   k N ⋅ m

Portanto,

53,75   d = 221,625

Logo,

d = 4,12   m

Resposta

d = 4,12   m

F R → = - 53,75 j ^   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As pás do ventilador portátil geram um empuxo T de 4N , como mostrado. Calcule o momento M O dessa força em relação ao ponto O na parte traseira da base. Para comparação, determine o momento em relaçã
Quatro forças são exercidas no olhal, como mostrado. Se o efeito resultante delas sobre o parafuso é um esforço trativo de 1200N na direção y , determine os valores necessários de T e θ .
O cubo da roda pode ser conectado ao eixo com deslocamento negativo (esquerda) ou com deslocamento positivo (direita). Se o pneu está sujeito às cargas normal e radial conforme mostrado, determine o m
Substitua o sistema de forças que age sobre a treliça por uma força e momento de binário resultante no ponto C .
Substitua o sistema de forças que age sobre a viga por uma força e momento de binário resultante no ponto B .