Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 156
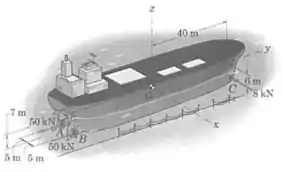
Um petroleiro se afasta das docas sob a ação do empuxo reverso da hélice , do empuxo para a frente da hélice e o empuxo lateral do motor . Determine o sistema força-binário equivalente no centro de massa .
Passo 1
Vamos começar escrevendo as forças em forma vetorial:
Agora vamos calcular a força resultante:
Passo 2
Beleza, já temos a força, agora falta o momento. As duas forças de na traseira formam um binário, que favorece a rotação em torno do eixo . Como elas estão separadas por uma distância de , o momento delas é:
Já a força de no ponto favorece a rotação em torno de dois eixos: o e o . A distância perpendicular até o eixo é de metros, já a distância até o eixo é de metros:
Passo 3
Agora podemos somar esses momentos:
Pronto!
Resposta
A força é e o momento é .
Exercícios de Livros Relacionados
A ação combinada das três forças sobre a base em O pode ser obtida estabelecendo sua resultante passando por O . Determine os módulos de R e do momento M associado.
Determine o momento da força P em relação ao ponto A .
Três binários são formados por três pares de forças iguais e opostas. Determine a resultante M dos três binários.
Quando o mastro O A está na posição mostrada, a força trativa no cabo A B vale 3k N .(a) Usando as coordenadas mostradas, escreva na forma vetorial a força trativa exercida na pequena arruela no ponto
Uma força F atua ao longo da linha A B dentro da casca cilíndrica circular, como mostrado. As quantidades r , h , θ e F são conhecidas. Usando as coordenadas x , y e z mostradas, expresse F como um ve