Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 27
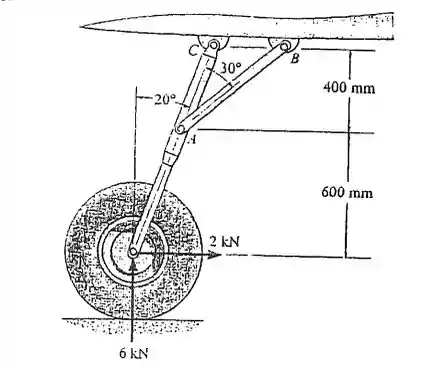
Quando os freios de um avião são acionados, a roda do nariz exerce duas forças sobre a extremidade do trem de pouso, como mostra a figura .Determine as componentes horizontal e vertical da reação no pino C e a força na escora AB
Passo 1
Salve salve galerinha do RespondeAí, tudo beleza? Saca só, nesse exercício aqui o enunciado nos disse que quando os freios de um avião são acionados, a roda do nariz exerce duas forças sobre a extremidade do trem de pouso, como na figura:
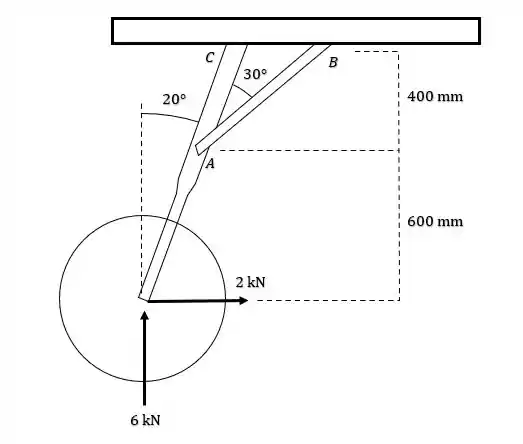
Sabendo disso, ele pediu pra gente encontrar as componentes horizontal e vertical da reação no pino e a força na escora .
Maravilha, como estamos falando de uma situação de equilíbrio, isso quer dizer que as forças verticais, horizontais e Momentos binários se anulam:
Passo 2
Show de bolinhas, então a primeira coisa que a gente deve fazer é esboçar o diagrama de corpo livre pro sistema vai ser dado como:
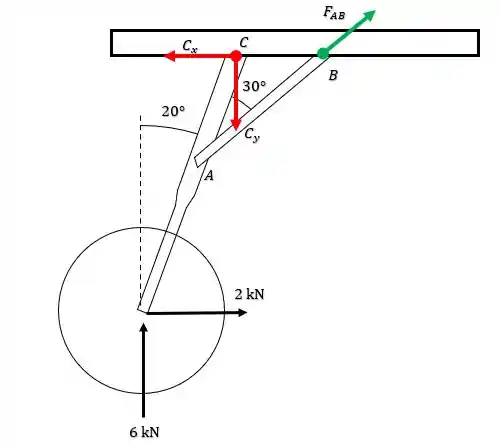
Então o somatório das forças em , será dado como:
Logo:
Agora fazendo o somatório das forças em , vamos obter que:
Então isolando :
Passo 3
Iradoso, agora se a gente fizer o somatório dos momentos em relação ao eixo da roda, vamos obter que:
Logo:
Substituindo os valores de e que a gente encontrou, vamos ter que:
Isolando , obtemos:
Passo 4
Belezoca, então substituindo esse resultado na equação para vamos obter:
Logo:
E para vamos ter que:
Logo:
Te vejo na próxima resolução
: )