Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 30
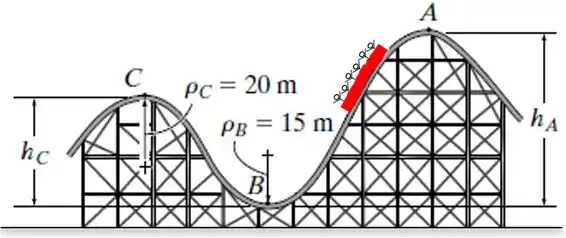
Se a pista deve ser projetada de maneira que os passageiros do carro da montanha-russa não sintam uma força normal igual a zero ou mais do que 4 vezes o seu peso, determine as altura limitantes e de maneira que isto não ocorra. O carro da montanha-russa parte do repouso na posição . Despreze o atrito.
Passo 1
O enunciado nos dá as seguintes informações:
Raio de cirvatira em m;
Raio de curvatura em m.
Além disso, ele nos diz que a força normal deve estar entre o intervalo:
Onde é a força peso.
A partir dessa condição, devemos determinar as alturas e , sabendo que o carrinho parte do repouso na posição , ou seja, .
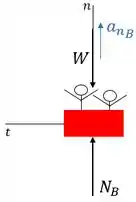
Inicialmente, vamos desenhar o diagrama de corpo livre do carrinho para o ponto e ponto , respectivamente:
Passo 2
Primeiramente, utilizaremos a Equação do Movimento no eixo :
O enunciado nos dá os valores de m e m. Sabemos que a aceleração normal é dada por:
Logo, para o ponto e , teremos
No ponto :
Neste ponto, a força normal será máxima, pois o carrinho estará no movimento de descida. Logo, .
Assim, temos que
No ponto
Neste ponto, como o carrinho estará subindo, a força normal tenderá a ser mínima, pois o carrinho estará na iminência de descolar da pista. Logo, .
Assim, temos que
Passo 3
Com as informaçãoes obtidas no passo anterior, podemos aplicar o Princípio do Trabalho e Energia para encontrar o valor das alturas e
No trecho :
A força normal não realiza trabalho pois age sempre perpendicurlamente ao deslocamento do carrinho. O trabalho será realizado pela força peso. Como o carrinho estará descendo, a força peso exercerá um trabalho positivo, pois age no mesmo sentido que o deslocamento.
Temos que:
onde
Substituindo esses valores na equação inicial, obtemos
No trecho :
A força normal não realiza trabalho pois age sempre perpendicurlamente ao deslocamento do carrinho. O trabalho será realizado pela força peso. Como o carrinho estará descendo, pois o ponto fica abaixo do ponto , a força peso exercerá um trabalho positivo, pois age no mesmo sentido que o deslocamento.
Temos que:
onde
Substituindo esses valores na equação inicial, obtemos