Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 32
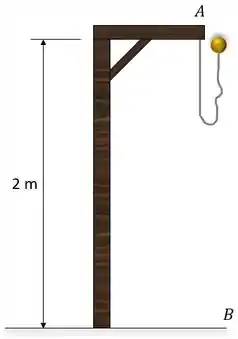
A bolas tem massa de 0,5 kg e está suspensa por uma tira de borracha que tem comprimento não deformado de 1 m e rigidez N/m. Se o apoio em ao qual a tira de borracha está ligada está a 2 m do solo, determine a maior velocidade que a bola pode ter em de maneira que ela não toque o solo quando alcança o seu ponto mais baixo . Despreze a dimensão da bola e a massa da tira de borracha.
Passo 1
O enunciado nos dá as seguintes informações:
Massa da bola: ;
Comprimento não deformardo da tira de borracha: ;
Rigidez da tira de borracha: ;
Altura do ponto .
Devemos determinar a maior velocidade que a bola pode ter em de maneira que ela não toque o solo em quando atingir seu ponto mais baixo, ou seja, quando a tira estiver esticada ao máximo.
Inicialmente, vamos desenhar o diagrama de corpo livre da bola para quando ela estiver no seu ponto mais baixo:
Onde é a força peso e é a força elástica exercida pela tira de borracha.
Passo 2
Vamos aplicar o Princípio do Trabalho e Energia para descobrir a velocidade máxima para que a bola não toque o solo.
Tanto a força elástica, quanto a força peso, atuam na mesma direção do deslocamento da bola, portanto ambas exercerão trabalho.
Porém, a força elástica age no sentido oposto ao deslocamento da bola, que está descendo em direção ao solo. Portanto, o trabalho exercido por ela será negativo.
No ponto mais baixo, a velocidade será nula (), pois o corpo estará na iminência de mudar o seu sentido de deslocamento.
O comprimento máximo da tira de borracha será igual à altura do ponto ().
Temos que,
onde
Substituindo esses valores na equação inicial, obtemos