Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 34
Se o coeficiente de atrito cinético entre a caixa de 100 kg e o plano é , determine a velocidade da caixa no instante que a compressão da mola é m. Inicialmente, a mola não está deformada e a caixa está em repouso.
Passo 1
O enunciado nos dá as seguintes informações:
Masas da caixa: ;
Coeficiente de atrito:
Rigidez da mola:
Velocidade inicial da caixa:
Compressão da mola: .
Devemos determinar a velocidade da mola no instante que a mola sofre uma compressão de m.
Inicialmente, vamos desenhar o diagrama de corpo livre da caixa em contato com a mola:
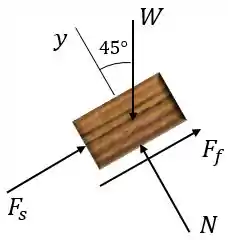
Onde é a força peso, é a força elástica da mola, é a força normal e é a força de atrito cinético.
Passo 2
Primeiramente, vamos encontrar o valor das forças normal e de atrito. Para isso, utilizaremos a Equação do Movimento:
No eixo de referência :
Logo, a força de atrito será igual a
Passo 3
Com os dados obtidos no passo anterior, podemos aplicar o Princípio do Trabalho e Energia para determinar a velocidade da mola quando m.
Na direção do deslocamento da caixa, temos a ação da força peso , força de atrito e força elástica . Porém, tanto a força de atrito quanto a força elástica agem no sentindo oposto ao deslocamento, portanto o trabalho exercido por elas será negativo.
Temos que,
onde
Substituindo esses valores na equação inicial e com os dados fornecidos pela questão, obtemos