Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 10
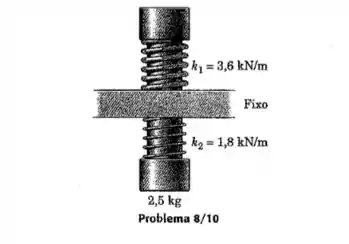
O pistão vertical possui uma massa de 2.5 kg e é sustentado pelas duas molas, que estão sempre em compressão. Calcule a frequência natural de vibração do pistão se ele é deslocado da posição de equilíbrio e liberado a partir do repouso. O atrito na guia é desprezível.
Passo 1
Bom, o enunciado nos diz que as molas estão sempre em compressão, mesmo nas situações de extremo (quando uma das molas está completamente comprimida, a outra ainda estará comprimida, mesmo que levemente). Assim, sempre haverá uma força restauradora vinda de cada mola mesmo para a situação de repouso do sistema, onde as forças resultam zero. Vamos escrever a segunda lei de Newton para esse caso:
Onde e são as forças de restauração de cada mola (sendo 1 a mola de cima e 2 a mola de baixo) independente do movimento oscilatório,
Passo 2
A segunda lei de Newton para o movimento oscilatório então será:
As forças e estão relacionadas com a restauração das molas quando elas comprimem além da compressão de cada uma no repouso do sistema.
Substituindo :
Reescrevendo:
Passo 3
Como o fator que multiplica o y é a frequência natural ao quadradom precisamos apenas convertê-la para a frequência de ciclos por segundo:
Substituindo os valores de cada grandeza: