Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 6
Para o sistema massa-mola mostrado, determine a deflexão estática , o período do sistema, e a velocidade máxima que resultam quando o cilindro é deslocado de 100mm para baixo a partir da sua posição de equilíbrio e solto.
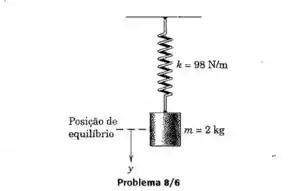
Passo 1
A deflexão estática pode ser obtida pela força peso e pela força da mola exercida sobre o corpo, pela Segunda Lei de Newton:
Onde x será a deflexão sobre a mola, e portanto a deflexão estática para o caso em que o sistema está em equilíbrio, então isolando x:
Passo 2
E então o cilindro é deslocado 100mm em relação ao equilíbrio anterior, para encontrarmos o período das oscilações vamos precisar encontrar a frequência do sistema, a equação da frequência é:
Substituindo todos os valores dados no enunciado:
Expressando a equação do período:
Resolvendo utilizando o valor que encontramos:
Passo 3
Para a velocidade, precisamos utilizar a equação da posição e derivá-la:
E para ela ser máxima, a função cosseno deve ser igual a 1, logo:
Como sabemos C, já que foi dito que o objeto foi deslocado 100 mm da posição de equilíbrio, e a frequência nos calculamos, basta substituir: