Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 7

O cilindro do Prob. 8/6 é deslocado de 100 mm para baixo a partir da suaposição de equilíbrio e solto no instante de tempo t = 0 . Determine a posição y , a velocidade v , e a aceleração a quando t = 3   s . Qual é a aceleração máxima?

Passo 1

Como a velocidade inicial não foi dada, nossa equação so depende da posição inicial, então a equação para y terá a seguinte forma:

y = y 0 c o s ω n t

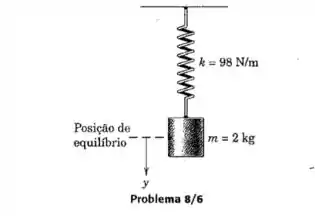
O cilindro é deslocado 100mm para baixo, supondo que a posição de equilíbrio é no nosso y = 0 , e orientado para baixo como na figura. Como a frequência foi calculada no problema anterior, a equação será:

y = 0.100 m c o s 0.7 t

Passo 2

A primeira derivada da função que descreve a posição, será a função da velocidade, então:

y ˙ = - ω n y 0 s e n ω n t

y ˙ = - 0 . 7 m / s s e n ⁡ ( ( 7 r a d / s ) t )

E a aceleração, como é a segunda derivada, será:

y ¨ = - ω n 2 y 0 c o s ω n t

y ¨ = - 0.7 r a d 2 0.100 m c o s ( ( 7 r a d / s ) t )

y ¨ = - 4.9 m / s 2 c o s ( ( 7 r a d / s ) t )

Passo 3

Agora, substituindo t = 3   s em cada uma das equações:

y = 0.100 m c o s 2 1 = - 0.0548 m

y ˙ = - 0.7 m / s s e n 21 = - 0.586   m / s

y ¨ = - 4.9 m / s 2 c o s 21 = 2.68 m / s 2

Passo 4

A aceleração máxima será o valor da amplitude da aceleração, ou quando a função cosseno é + ou = 1:

y ¨ m a x = 4.9 m / s 2

Resposta

y = - 0.0548 m

y ˙ = - 0.586   m / s

y ¨ = 2.68 m / s 2

y ¨ m a x = 4.9 m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

36. Para o sistema massa-mola amortecido mostrado, determine o coeficiente de amortecimento viscoso para o qual ocorrerá um amortecimento crítico
39. Um aperfeiçoamento posterior do projeto para a plataforma de pesagem do problema 8.14 é apresentado aqui, onde dois amortecedores viscosos foram adicionados para limitar a razão de sucessivas ampl
38. Se a amplitude do oitavo ciclo de um oscilador linear com amortecimento viscoso é dezesseis vezes a amplitude do vigésimo ciclo, calcule o fator de amortecimento ξ .
44. O proprietário de uma caminhonete de 1660k g testa a ação dos amortecedores traseiros aplicando uma força constante de 450N ao para-choque traseiro e medindo um deslocamento estático de 75m m . Ap
43. A massa do sistema apresentado é liberada a partir do repouso em x 0 = 150m m , quando t = 0 . Determine o deslocamento x em t = 0,5s , se (a) c = 200N ⋅ s / m e (b) 300N ⋅ s / m .