Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 10
O conjunto mostrado na figura consiste uma haste reta que passa através de uma placa retangular e está soldada. O conjunto gira em torno do eixo com uma velocidade angular constante de . Sabendo que a rotação é no sentido anti-horário quando vista de , determine a velocidade e a aceleração do canto .
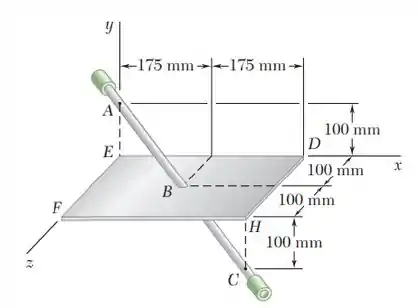
Passo 1
Fala aí, galerinha. Tudo beleza? Bora para mais um exercício de Dinâmica. Neste problema, temos que determinar a velocidade e a aceleração do canto . Para isso, vamos primeiro determinar o vetor , ele é dado por:
E o seu módulo vai ser:
Com isso, podemos expressar a velocidade angular a partir do conceito de vetor unitário. Sendo assim, temos que:
Assim, podemos encontrar o vetor velocidade em função do eixo, ele é dado por:
Passo 2
Em seguida, sabemos que a velocidade de um ponto qualquer de um corpo que gira em torno de um eixo fixo é dado pela seguinte relação:
Onde é a aceleração angular do corpo e é o vetor de posição desenhado a partir de qualquer ponto sobre o eixo de rotação do ponto. Neste caso, ou seja, para o ponto , o vetor posição vai ser:
Assim, para encontrarmos a velocidade do ponto , temos que:
Passo 3
Por fim, para encontrarmos a aceleração no ponto temos que usar a seguinte relação:
Como o problema nos informa que não há aceleração angular, temos que:
É isso, galerinha. Bora praticar mais!