Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 62

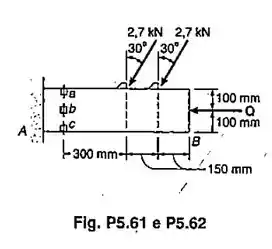
A viga em balanço AB tem uma seção transversal retangular de 90 x 200 mm. Determinar: (a) o valor da força axial Q para que a tensão normal no ponto c seja -5,5 MPa; (b) as correspondentes tensões, normal e de cisalhamento, no ponto b.

Passo 1

Dessa questão temos que seção é de 90 x 200 mm

Calculando então as forças em x

F x = 2,7 × c o s 60 = 1,35   k N

Agora forçar em Y

F y = 2,7 × c o s 30 = 2,338   k N

Vamos analizar agora o momento fletor e calcular o momento de inpercia

M = 2,7 × 10 3 × 0,45 + 2,7 × 10 3 × 0,3 - 1,35 × 10 3 × 0,1 × 2 = 1483,5   N . m

I = 1 12 × 0,09 × 0,2 3 = 6 × 10 - 5 m 4

Passo 2

a) Com esses dados em mão podemos começar a analisar o que o enunciado pede. Para determinarmos o valor da força axial Q faremos

σ = - P A - M x I - Q A

O enunciado nos afirma que σ = - 5,5 × 10 6 ,   então

- 5,5 × 10 6 = - 2,7 × 10 3 0,09 × 0,2 - 1483,5 × 0,1 6 × 10 - 5 - Q 0,09 × 0,2

- 5,5 × 10 6 = - 150 × 10 3 - 2,473 × 10 6 - Q 0,018

Q = 51,786   k N

A letra (b) nos pede as tensões normais e de cisalhamento no ponto b. Vamos lá então

Analisando agora o ponto b

Para calcularmos o τ precisamos antes do valor de Q τ ,   então

Q τ = y - × A = 0,09 × 0,1 × 0,05 = 4,5 × 10 - 4 m 3  

Então τ fica

τ = V Q τ I t = 2 × 2,338 × 10 3 4,5 × 10 - 4 6 × 10 - 5 0,09 = 0,39   M P a

σ = - P A - Q A = - 2,7 × 10 3 0,09 × 0,2 - 51,786 × 10 3 0,09 × 0,2 = - 3,027   M P a

Resposta

a )   Q = 51,786   k N

b )   τ = 0,39   M P a

σ = - 3,027   M P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga simplesmente apoiada é composta por duas seções W310x33 montadas como mostra a figura. Determine a carga uniforme máxima w que ela suportará se a tensão de flexão admissível for σ a d m = 160M
Selecione no apêndice B a viga de aço de abas largas de menor peso que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é σ a d m = 160M P a e atenção de cisalhamen
A viga será usada para suportar uma máquina que tem peso de 80k N e centro de gravidade em G. Se a tensão de flexão máxima não puder ultrapassar σ a d m = 160M P a , determine a largura b exigida para
A viga composta foi feita com duas seções unidas por um pino em B. Use o Apêndice B e selecione a viga de abas largas leve que seria segura para cada seção, se a tensão de flexão admissível for σ a d
A viga de madeira tem seção transversal retangular. Se sua largura for 150 mm, determine a altura h de modo que atinja simultaneamente sua tensão de flexão admissível σ a d m = 10M P a e uma tensão de