Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 188

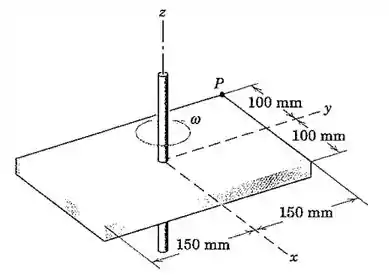
A placa retangular gira em torno de seu eixo fixo z. No instante considerado sua velocidade angular é ω = 3   r a d / s e está diminuindo na taxa de 6 rad/s por segundo. Para esse instante escreva as expressões vetoriais para a velocidade de P e suas componentes normal e tangencial da aceleração.

Passo 1

Bom pessoal, nesta questão basta utilizar os conceitos aprendidos ao longo do capítulo. Vamos primeiro escrever a posição de P na forma vetorial:

r = - 0,1 i + 0,15 j   m  

A velocidade absoluta e a velocidade angular de um eixo que rotacional podem ser relacionadas pela equação:

v = ω × r

v = 3 k ^ × - 0,1 i + 0,15 j   = - 0,45 i - 0,3 j   m / s

Já a aceleração possui duas componentes:

- Aceleração normal: possui a mesma direção do vetor posição, mas sentido contrário. Pode ser calculada por:

a n = ω × v = 3 k × - 0,45 i - 0,3 j = 0,9 i - 1,35 j   m / s 2  

- Aceleração tangencial: é perpendicular ao vetor posição. Pode ser calculada por:

a t = α × r = - 6 k × - 0,1 i + 0,15 j   = 0,9 i + 0,6 j   m / s 2

OBS: o sentido de α é negativos, pois a placa está freiando.

Resposta

v = 0,45 i - 0,3 j   m / s

a n = 0,9 i - 1,35 j   m / s 2

a t = 0,9 i + 0,6 j   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

54. O pinhão A roda sobre a cremalheira fixa B com uma velocidade angular ω = 4 r a d s . Determine a velocidade da cremalheira C.
O anel semicircular uniforme de massa m = 2,5k g e raio médio r = 200m m está montado sobre raios de massa desprezível e gira em torno de um eixo horizontal através de O . Se o anel é liberado a parti
O cilindro maciço homogêneo possui uma massa de 100k g e está montado em um eixo em ângulo reto que gira livremente em torno do eixo horizontal O - O . Se o cilindro é liberado a partit do repouso com
A massa da engrenagem A é de 20k g e seu raio de giração centroidal é de 150m m . A massa da engrenagem B é de 10k g e seu raio de giração centroidal é de 100m m . Calcule a aceleração angular da engr
O anel semicircular de massa m e raio r está soldado no eixo vertical, que permite que o anel gire no plano horizontal em torno do eixo O - O . Se um torque M é aplicado ao anel por meio de seu eixo,