Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 51

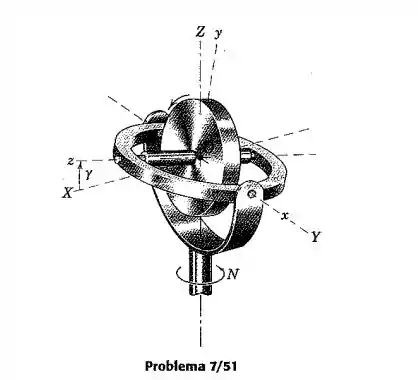
O rotor do giroscópio mostrado está girando na taxa constante de 100 rpm em relação aos eixos x - y - z , no sentido indicado. Se o ângulo γ entre o anel de suspensão e o plano horizontal X - Y é levado a aumentar à taxa constante de 4   r a d / s e se a unidade é obrigada a realizar precessão em relação à vertical na taxa constante N = 20   r p m , calcule o módulo da aceleração angular α do rotor quando γ = 30 º . Resolva utilizando a Eq. 7/7 aplicada à velocidade angular do rotor.

Passo 1

Para resolvermos o problema, vamos usar as relações já vistas de velocidade relativa e aceleração relativa, além da equação 7/7 onde a mesma nos dá a aceleração em um outro referencial como é pedido no problema.

Passo 2

Vamos começar coletando todos os dados que temos. Temos que Ω é nossa velocidade angular dos eixos e que ω é a velocidade angular do sistema. Sabemos que a velocidade do sistema é dada pela soma da velocidade do rotor com a velocidade angular dos eixos, assim temos que:

ω = Ω + ω r o t o r = Ω + 100 ⋅ 2 ⋅ π 60 ⋅ k ^

Nosso Ω é a soma da velocidade de todos os eixos, assim Ω = γ ˙ + ω 1 . Onde ω 1 é a velocidade angular da precessão que é causada pelo sistema. Mas temos que conforme é feita a precessão, essa velocidade irá variar com o ângulo γ . Logo, ω 1 = ω 1 ⋅ cos ⁡ γ ⋅ j ^ + ω 1   ⋅ s e n γ ⋅ k ^ . Substituindo na equação acima, chegamos que:

Ω = - γ ˙ ⋅ i ^ + ω 1 ⋅ cos ⁡ γ ⋅ j ^ + ω 1 ⋅ s e n γ ⋅ k ^

Usando agora a equação sugerida, temos que:

α = d ω d t X Y Z = d ω d t x y z + Ω × ω

Mas temos também que d ω d t x y z pode ser escrito da seguinte forma:

d ω d t x y z = d Ω d t x y z + Ω × Ω = - γ ˙ ⋅ ω 1 ⋅ s e n γ ⋅ j ^ + γ ˙ ⋅ ω 1 ⋅ c o s γ ⋅ k ^

Ω × ω = Ω ⋅ Ω × p ⋅ k ^ = γ ˙ ⋅ j ^ + p ⋅ ω 1 ⋅ cos ⁡ γ ⋅ i ^

Substituindo os valores e realizando a conversão para r a d / s   para o caso de ω 1 , vamos ter que:

α = γ ˙ ⋅ p - γ ˙ ⋅ p ⋅ s e n γ ⋅ j ^ + p ⋅ ω 1 ⋅ cos ⁡ γ ⋅ i ^ + γ ˙ ⋅ ω 1 ⋅ c o s γ ⋅ k ^

α = 4 ⋅ 10 ⋅ π 3 - 4 ⋅ 2 ⋅ π 3 ⋅ 1 2 ⋅ j ^   r a d / s 2 + 10 ⋅ π 3 ⋅ 2 ⋅ π 3 ⋅ 3 2 ⋅ i ^ + 4 ⋅ 2 ⋅ π 3 ⋅ 3 2 ⋅ k ^   r a d / s 2  

α = 18.99 ⋅ i ^ + 37.70 ⋅ j ^ + 7.25 ⋅ k ^   r a d / s 2  

Calculando o módulo desse vetor, chegamos que:

α = 42.8   r a d / s 2

Resposta

Resposta: α = 42.8   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

105. A caixa retangular de paredes finas com extremidades abertas, de seção transversal quadrada, está girando no espaço em torno de seu eixo longitudinal central como mostrado. Se o eixo sofre uma li
103. O rotor de 210k g do motor de um avião turbojato tem um raio de giração de 220m m e gira no sentido anti-horário a 18000r p m quando visto de frente. Se o avião está viajando a 1200k m / h e come
100. O ventilador para uma aplicação especial é montado conforme mostrado. O rotor do motor, o eixo e as pás têm uma massa combinada de 2,2k g com raio de giração de 60m m . A posição axial b do bloco
104. Um pequeno compressor de ar para a cabine de um avião é composto pela turbina A de 3,50k g , que aciona o soprador B de 2,40k g a uma velocidade de 20000r p m . O eixo do conjunto está montado tr
Determine o momento de inércia da pirâmide homogênea de massa m em relação ao eixo z . A densidade do material é ρ . Sugestão: utilize um elemento de placa retangular tendo um volume d V = 2 x 2 y d z