Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 114
A placa retangular é suportada por dobradiças ao longo de seu lado e pelo cabo . Se a força trativa no cabo vale , determine a projeção sobre a linha da força exercida pelo cabo sobre a placa. Note que é o ponto médio da borda horizontal superior do suporte estrutural.
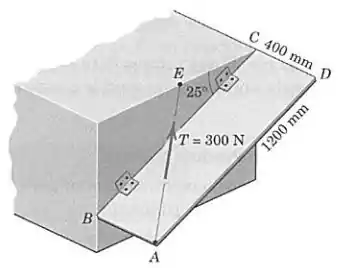
Passo 1
Para escrever os vetores, vamos considerar os eixos , e conforme representados na figura a seguir:
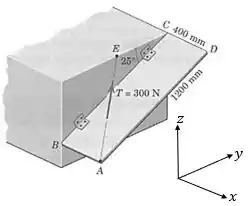
Sendo assim, vamos escrever a força trativa em sua forma vetorial:
onde e é o vetor unitário que sai de em direção a , ou seja, na mesma direção e sentido de :
Passo 2
Podemos determinar a projeção sobre a linha da força exercida pelo cabo sobre a placa calculando o produto escalar entre o vetor que acabamos de obter e o vetor unitário , que sai de em direção a :
Resposta
Exercícios de Livros Relacionados
133. Dois cabos exercem forças sobre o tubo. Determine a intensidade da componente projetada de F 1 ao longo da linha de ação de F 2 .
137. Determine o ângulo θ entre os segmentos de tubo B A e B C .
134. Determine o ângulo θ entre os dois cabos conectados ao tubo.
136. determine a intensidade da componente projetada da força de 500N que atua ao longo do eixo B C do tubo.
Um balão de propaganda está amarrado a um suporte por um cabo que tem uma massa de 0,12 kg/m. Com o vento, as forças trativa em A e B são de 110 N e 230 N, respectivamente. Determine a altura h do bal