Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 30

O bloco de 50 kg é transportado por uma distância curta, usando-se dois rolos cilíndricos, cada um com massa de 17,5 kg. Se uma força horizontal P = 125 N é aplicada ao bloco, determine a velocidade dele após haver se deslocado 0,6 m para a esquerda. Originalmente o bloco está em repouso. Não há deslizamento.

Passo 1

Começaremos o exercício calculando o valor da velocidade angular das rodas e da velocidade do centro de massa da mesma, tudo em função da velocidade de linear das rodas:

ω = v B r B = v B 0,9 → ω = 1,111   v B

v G = r G r B v B = 0,45 0,9 v B → v G = v B 2

O momento de inércia da roda com relação ao seu centro de massa é dada por:

I G = 1 2 m r 2 = 1 2 17,5 0,45 2 → I G = 1,772   k g . m 2

Sendo assim, a energia cinética do sistema é dada por:

T = T A + 2 T B

T = 1 2 m A v B 2 + 2 1 2 I G ω 2 + 1 2 m C v G 2 = 1 2 50 v B 2 + 2 1 2 1,772 v B 3 2 + 1 2 17,5 v B 2 2

T = 29,572 v B 2

Passo 2

Como o sistema está inicialmente em repouso, T 1 = 0 , e com base na figura a seguir:

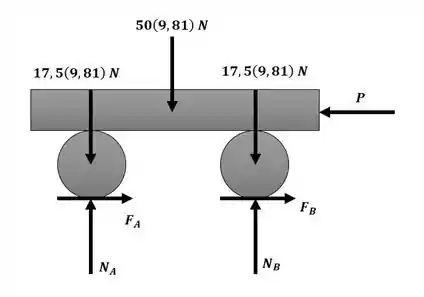
Sabemos que F A ,   F B ,   N A ,   N B e os pesos não realizam trabalho, equanto a força P realiza, sendo assim, quando o bloco se desloca s P = 2   m , o trabalho realizado pela força P é dado por:

U P = P s P = 1 25 2 → U P = 250   J

Passo 3

Agora iremos aplicar o princípio do trabalho e da energia:

T 1 + ∑ U 1 - 2 = T 2

0 + 250 = 29,572 v B 2

v B = 2,91   m / s

Resposta

v B = 2,91   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um foguete de massa m é lançado verticalmente da superfície da Terra, ou seja, em r = r 1 . Suponha que nenhuma massa é perdida à medida que ele se desloca para cima, determine o trabalho que ele prec
A força F , atuando em uma direção constante sobre o bloco de 20 kg, tem uma intensidade que varia com a posição s do bloco. Determine a velocidade do bloco após ele deslizar 3 m. Quando s = 0 , o blo
A força F , atuando em uma direção constante sobre o bloco de 20 kg, tem uma intensidade que varia com a posição s do bloco. Determine a distância que o bloco desliza antes que sua velocidade se torne
O cilindro tem massa de 10 kg e é empurrado contra uma série de molas prato Belleville de maneira que a compressão na mola é s = 0,015 m. Se a força da mola sobre o cilindro é F = ( 750s 1 / 3 ) N, on
O carro de 2 Mg tem uma velocidade v 1 = 100k m / h quando o motorista vê um obstáculo na frente do carro. Leva 0,75 s para ele reagir e travar os freios completamente, fazendo com que o carro derrape